Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có:

Ta thấy hai vectơ \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \) cùng hướng nên \(\left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right) = 0^\circ \)
\( \Rightarrow \overrightarrow {OA} .\overrightarrow {OB} = \left| {\overrightarrow {OA} } \right|.\left| {\overrightarrow {OB} } \right|.\cos \left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right) = a.b.\cos 0^\circ = ab\)
b) Ta có:

Ta thấy hai vectơ \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \) ngược hướng nên \(\left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right) = 180^\circ \)
\( \Rightarrow \overrightarrow {OA} .\overrightarrow {OB} = \left| {\overrightarrow {OA} } \right|.\left| {\overrightarrow {OB} } \right|.\cos \left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right) = a.b.\cos 180^\circ = - ab\)

A B C D O I J
a) Theo tính chất trung điểm ta có:
\(\overrightarrow{OI}=\dfrac{1}{2}\left(\overrightarrow{OA}+\overrightarrow{OB}\right)\).
b) Có \(k=\dfrac{OD}{OA}\) nên \(\overrightarrow{OD}=k\overrightarrow{OA}\).
Theo định lý Ta-lét\(\dfrac{OD}{OA}=\dfrac{OB}{OC}\). Vì vậy \(\overrightarrow{OB}=k\overrightarrow{OC}\).
Áp dụng tính chất trung điểm:
\(\overrightarrow{OJ}=\dfrac{1}{2}\left(\overrightarrow{OD}+\overrightarrow{OC}\right)=\dfrac{1}{2}\left(k\overrightarrow{OA}+k\overrightarrow{OB}\right)\)\(=\dfrac{k}{2}\left(\overrightarrow{OA}+\overrightarrow{OB}\right)\).
Suy ra: \(\overrightarrow{OI}=\dfrac{k}{2}\overrightarrow{OJ}\) và dễ thấy \(k\ne0\) nên 3 điểm O, I, J thẳng hàng.

Do \(\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{0}\) nên hai véc tơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) đối nhau.
a)
\(\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{0}\) nên O là trung điểm của AB.
b) \(\overrightarrow{OB}=\overrightarrow{OA}+\overrightarrow{AB}=\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{0}\) nên \(O\equiv B\).

a) Giả sử véc tơ \(\overrightarrow{OA}+\overrightarrow{OB}\) nằm trên đường phân giác góc \(\widehat{AOB}\) .
Dựng hình bình hành OABD.
O A B D
Theo quy tắc hình bình hành: \(\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{OD}\).
Theo giả thiết thì OD là tia phân giác góc \(\widehat{AOB}\).
Vì vậy hình bình hành OABD là hình thoi.
Suy ra OA = OB.
- Giả sử OA = OB.
Khi đó hình bình hành OABD có OA = OB nên tứ giác OABD là hình thoi.
Kết luận: Điều kiện cần và đủ để véc tơ \(\overrightarrow{OA}+\overrightarrow{OB}\) nằm trên đường phân giác góc \(\widehat{AOB}\) là OA = OB.

câu 2 ( các kí hiệu vecto khi lm bài thỳ b tự viết nhé mk k viết kí hiệu để trả lời cho nhanh hỳ hỳ )
OA+ OB + OC = OA'+ OB' + OC'
<=> OA - OA' + OB - OB' + OC - OC' = 0
<=> A'A + B'B + C'C = 0
<=> 2 ( BA + CB + AC ) = 0
<=> 2 ( CB + BA + AC ) = 0
<=> 2 ( CA + AC ) = 0
<=> 0 = 0 ( luôn đúng )
câu 1 ( các kí hiệu vecto b cx tự viết nhá )
VT = OD + OC = OA + AD + OB + BC = OA + OB + AD + BC = BO + OB + AD + BC = 0 + AD + BC = AD + BC = VP ( đpcm)

\(\overrightarrow{AC}-\overrightarrow{AD}=\overrightarrow{AC}-\overrightarrow{BC}=\overrightarrow{AC}+\overrightarrow{CB}=\overrightarrow{AB}\)
Đáp án A đúng
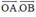 trong hai trường hợp:
trong hai trường hợp: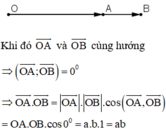


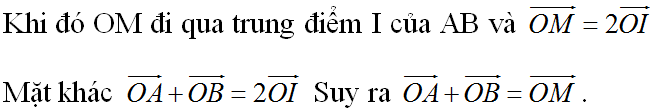
a) Khi O nằm ngoài đoạn AB thì hai vec tơ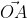 và
và 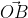 cùng hướng và góc
cùng hướng và góc
(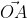 ,
, 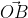 ) = 0
) = 0
cos(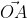 ,
, 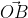 ) = 1 nên
) = 1 nên 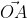 .
.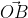 = a.b
= a.b
b) Khi O nằm ngoài trongđoạn AB thì hai vectơ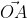 và
và 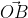 ngược hướng và góc
ngược hướng và góc
(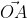 ,
, 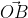 ) = 1800
) = 1800
cos(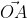 ,
, 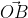 ) = -1 nên
) = -1 nên 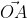 .
.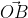 = -a.b
= -a.b
Cảm phiền bác đăng lớp 6,7 được không ạ -.-