

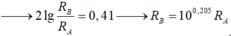
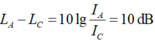
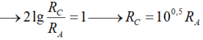
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


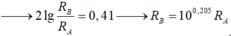
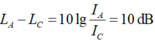
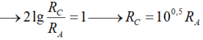
![]()
![]()
![]()
![]()

Chọn đáp án A
Giả sử nguồn âm tại O có công suất P: I = P 4 π R 2
Hiệu mức cường độ âm giữa hai điểm A, B: L A − L B = 10 lg I A I B = 4 , 1 d B ⇒ 2 lg R B R A = 0 , 41 ⇒ R B = 10 0 , 205 R A

+ Giả sử nguồn âm tại O có công suất P: I = P 4 π R 2
+ Hiệu mức cường độ âm giữa hai điểm A, B: L A − L B = 10 lg I A I B = 4 , 1 d B ⇒ 2 lg R B R A = 0 , 41 ⇒ R B = 10 0 , 205 R A
Chọn đáp án A

Mạch chỉ có điện trở thuần thì u cùng pha với i.
Nếu \(u=U_0\cos\left(\omega t+\varphi\right)\)
Thì: \(i=I_0\cos\left(\omega t+\varphi\right)\)
\(\Rightarrow\frac{u}{U_0}=\frac{i}{I_0}\)
\(\Rightarrow\frac{u^2}{U_0^2}+\frac{i^2}{I_0^2}=1\) là sai.

\(\omega=\frac{2\pi}{T}=2\pi\)(rad/s)
Vận tốc cực đại \(v_{max}=\omega A=2\pi.5=10\pi\)(cm/s)
Vì vận tốc là đại lượng biến thiên điều hòa theo thời gian, nên ta khảo sát nó bằng véc tơ quay.
10π v 5π M N -10π O
Tại thời điểm t, trạng thái của vận tốc ứng với véc tơ OM, sau 1/6 s = 1/6 T, véc tơ quay: 1/6.360 = 600
Khi đó, trạng thái của vận tốc ứng với véc tơ ON --> Vận tốc đạt giá trị cực đại là: \(10\pi\) (cm/s)
Đáp án B.

Khoảng cách ngắn nhất giữa hai gợn lồi liên tiếp là \(\frac{\lambda}{2} \Rightarrow \lambda = 2.2=4cm\)
Số gợn lồi (dao động cực đại) là số giá trị k thỏa mãn: \(-S_{1}S_{2}< k \lambda < S_{1}S_{2}\Rightarrow -4.125 < k < 4.125\\ \Rightarrow k = -4,-3,-2,-1,0,1,2,3,4\)
=> có 9 gợn lồi.
Số gợn lõm (dao động cực tiểu) là số giá trị k thỏa mãn: \(-S_{1}S_{2}< (k+0.5) \lambda < S_{1}S_{2}\Rightarrow -4.125 < k+0.5 < 4.125\\ \Rightarrow -4.625 < k < 3.625 \\ \Rightarrow k = -4,-3,-2,-1,0,1,2,3.\)
=> có 8 gợn lõm.

+ Ban đầu M là vân tối thứ 3 nên: \(x_M=\left(2+\frac{1}{2}\right)\frac{\lambda D}{a}\left(1\right)\)
+ Khi giãm S1S2 một lượng \(\Delta\)a thì M là vân sáng bậc n nên: \(x_M=n\frac{\lambda D}{a-\Delta a}\left(2\right)\)
+ Khi tăng S1S2 một lượng \(\Delta\)a thì M là vân sáng bậc 3n nên: \(x_M=3n\frac{\lambda D}{a+\Delta a}\left(3\right)\)
+ (2) và (3) \(\Rightarrow k\frac{\lambda D}{a-\Delta a}=3k\frac{\lambda d}{a+\Delta a}\Rightarrow\Delta a=\frac{a}{2}\)
+ Khi tăng S1S2 một lượng 2\(\Delta\)a thì M là sáng bậc k nên: \(x_M=k\frac{\lambda D}{a+2\Delta a}=2,5\frac{\lambda D}{a}\left(4\right)\)
+ Từ (1) và (4) \(\Rightarrow\) k = 5. Vậy tại M lúc này là vân sáng bậc 5.