Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

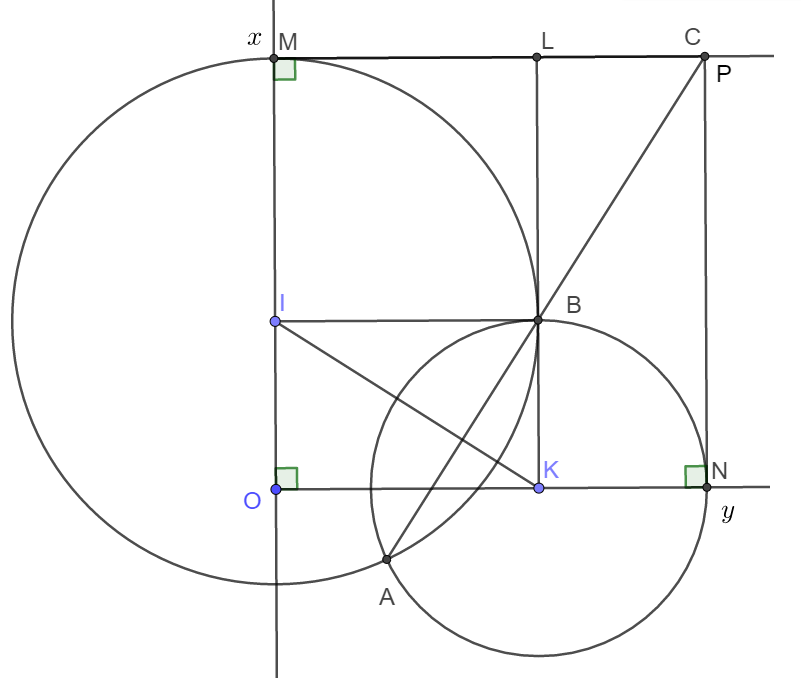
a) Trong tam giác OIK có:
|OK −− OI| < IK < |OK + OI| hay ∣R−r∣<IK<∣R+r∣∣R−r∣<IK<∣R+r∣.
Vậy hai đường tròn (I) và (K) luôn cắt nhau.
b) Dễ thấy tứ giác OMCN là hình chữ nhật (Tứ giác có 3 góc vuông).
Mà OM = OI + IM = OI + OK;
ON = OK + KN = OK + OI.
Vậy OM = ON hay hình chữ nhật OMCN là hình vuông.
c) Gọi giao điểm của BK và MC là L và giao điểm của AB với MC là P.
Tứ giác IBKO là hình chữ nhật. Suy ra IB = OK.
Tứ giác MLBI là hình vuông nên ML = BI, BL = OK.
Từ đó suy ra ΔBLP=ΔKOIΔBLP=ΔKOI. Vì vậy LP = OI.
Suy ra MP = ON = MC. Hay điểm C trùng với P.
Suy ra ba điểm A, B, C thẳng hàng.
d) Nếu OI + OK = a (không đổi) thì OM = MC = a không đổi. Suy ra điểm C cố định.
Vậy đường thẳng AB luôn đi qua điểm C cố định.

Bài của bạn hay, nhưng bạn viết phần 2/ ẩu quá!.
Câu 1. Vì O là tâm đường tròn qua hai điểm A,B nên \(OA=OB\to O\) nằm trên trung trực của đoạn thẳng AB cố định. Đảo lại với mỗi điểm O nằm trên trung trực AB, ta vẽ đường tròn tâm O bán kính OA thì đường tròn này đi qua AB.
Câu 2. Vì IJ là đường kính của đường tròn (O) nên \(JM\perp CI,IN\perp CJ,CE\perp JI\) do đó ba đường thẳng \(JM,CE,IN\) là ba đường cao của tam giác \(CJI\to\) ba đường này đồng quy tại trực tâm tam giác \(CJI.\) Vậy \(D\) nằm trên đường thẳng AB.
Gọi F là giao điểm của tiếp tuyến tại M với đường thẳng AB. T
a có \(\angle FMC=90^{\circ}-\angle OMI=90^{\circ}-\angle OIM=\angle ECI=\angle MCF\to\Delta FMC\) cân ở F. Mà tam giác MCD vuông ở M nên \(\angle FMD=\angle FDM\to\Delta DFM\) cân ở F. Thành thử \(F\) là trung điểm CD. Vậy tiếp tuyến ở M cắt CD tại trung điểm của CD. Tương tự chứng minh được tiếp tuyến tại N của (O) cũng đi qua trung điểm của CD. Vậy hai tiếp tuyến tại M,N cắt nhau ở tại trung điểm CD.