Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu hỏi của tran thi nga - Toán lớp 4 - Học toán với OnlineMath
co hai to giay hình vuông mà số đo các cạnh hơn kém nhau 8cm.đem đặt tờ giáy hình vuông nhỏ nằm trọn trong to giay hinh vuong lớn thì diện tích còn lại không bị chei của tờ giay là 96cm2.Tính cạnh mỗi tờ giay
Khi đặt 2 từ giấy lên nhau ta sẽ được một hình như hình vẽ trên.
Qua hình vẽ trên ta thấy phần giấy của tờ lớn không bị che lấp tương ứng với 2 hình chữ nhật (gạch chéo) có một cạnh 7cm và cạnh còn lại bằng cạnh tờ giấy nhỏ và một hình vuông nhỏ (1) có cạnh là 7cm
Diện tích 1 hình chữ nhật (gạch chéo) là : .................
Cạnh hình vuông nhỏ là : ... : 7
Cạnh hình vuông lớn là : ... + 7
AI XEM RỒI NHỚ ĐỂ LẠI 1 L-I-KE CHO BÀI TRÊN ![]()
MÌNH CŨNG ĐỒNG Ý VỚI Ý KIẾN CỦA Songoku Sky Fc11 NHƯNG BẠN CÓ BỊ SAO KO CÂU CUỐI CÙNG BẠN GIẢI RA ĐƯỢC KO VIẾT VẬY KHÔNG AI HIỂU ĐÂU NHƯNG CẢM ƠN BẠN VÌ BẠN ĐÃ GIAIRVIF BÀI NÀY MÌNH CŨNG THẮC MẮC

Bài này nếu ở tiểu học thì phải vẽ hình; còn lớp 9 thì tôi thử làm như sau:
Gọi cạnh của tờ giấy lớn là a cm; cạnh tờ giấy nhỏ là b cm (a > b; a và b là STN)
Diện tích của tờ giấy lớn là a2 cm2; cạnh tờ giấy nhỏ là b2 cm2
Theo bài ra ta có: a2 - b2 = 63
<=> (a + b) (a-b) = 63
Vì 63 = 1.63 = 3. 21 = 7.9 nên xảy ra các trường hợp:
* TH1: a + b = 63 và a - b = 1 => a =32 cm; b = 31 cm
* TH2: a + b = 21 và a - b = 3 => a = 12cm; b = 9cm

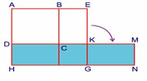
Ta đặt tấm bìa hình vuông nhỏ lên tấm bìa hình vuông lớn sao cho cạnh hình vuông nhỏ trùng khít với cạnh hình vuông lớn. Gọi hai hình vuông là ABCD và AEGH. Diện tích phần tấm bìa không bị chồng lên bao gồm hai hình chữ nhật BCKE và DKGH. Hai hình chữ nhật này có BE = DH (chính là hiệu số đo các cạnh của hai hình vuông). Chuyển hình chữ nhật BCKE xuống bên cạnh hình chữ nhật DKGH ta được hình chữ nhật GKMN. Khi đó ta có diện tích hình chữ nhật HDMN là 63 c m 2 . Ta thấy hình chữ nhật HDMN có chiều dài và chiều rộng chính là tổng và hiệu số đo hai cạnh hình vuông. Vì hai hình vuông đều có số đo các cạnh là số tự nhiên chia hết cho 3, nên tổng và hiệu số đo hai cạnh hình vuông cũng phải là số chia hết cho 3. Do đó chiều dài và chiều rộng của hình chữ nhật HDMN đều là số chia hết cho 3.
Vì 63 = 1 x 63 = 3 x 21 = 7 x 9 nên chiều dài và chiều rộng của hình chữ nhật HDMN phải là 21 cm và 3 cm.
Vậy độ dài cạnh của tấm bìa hình vuông nhỏ là : (21 - 3) : 2 = 9 (cm)
Độ dài cạnh của tấm bìa hình vuông lớn là : 9 + 3 = 12 (cm)

Giả sử tờ giấy lớn có cạnh là a, tờ giấy nhỏ có cạnh là b
Diện tích còn lại của tờ giấy lớn là tổng diện tích 2 hình chữ nhật (1) và (2)
Diện tích hình chữ nhật (1) là:
(a-b) x b
Diện tích hình chữ nhật (2) là:
(a-b) x a
Tổng diện tích 2 hình chữ nhật đó là:
(a-b)xb+(a-b)xa = (a-b).(a+b) = 63 (cm2)
Mà 63 = 63x1 = 21x3 = 9x7
Ta có các trường hợp có thể xảy ra là Tổng và Hiệu của a và b.
a-b=1 và a+b=63 Suy ra a=(63+1):2 = 32 ; b=63-32=31
a-b=3 và a+b=21 Suy ra a=(21+3):2 = 12 ; b=21-12=9
a-b=7 và a+b=9 Suy ra a=(9+7):2 = 8 ; b=9-8=1
Đáp số:
a=32 và b=31
a=12 và b=9
a=8 và b=1

Gọi độ dài lớn nhất của cạnh hình vuông là a ( cm )
Vì 75 cm và 105 cm được chia đều cho a ( cm )
=> 75⋮a;105⋮a => a ∈ ƯC 75,105
Mà a là lớn nhất => a = ƯCLN ( 75 , 105 )
Ta có : 75 = 3 . 52
105 = 3 . 5 . 7
ƯCLN ( 75 , 105 ) = 3 . 5 = 15
=> a = 15 Vậy độ dài lớn nhất của cạnh hình vuông là 15 cm
Để cắt hết tấm bìa thành những hình vuông bằng nhau thì độ dài cạnh hình vuông phải là một ước chung của chiều rộng và chiều dài của tấm bìa. Do đó muốn cho cạnh hình vuông là lớn nhất thì độ dài của cạnh phải là ƯCLN (75, 105).
Vì 75 = 3 . 52 ; 105 = 3 . 5 . 7 nên ƯCLN (75, 105) = 15.
Ta gọi cạnh hình vuông lớn là a, hình vuông bé là b
Ta có : a x a - b x b = 31
Ta liệt kê các số = a x a hoặc b x b, sau đó ta sẽ tìm 2 số có hiệu = 31 :
1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, ...
Vậy ta tìm được cặp số 225 - 256 có hiệu = 31
Diện tích hình bé là 225 cm2, diện tích hình lớn là 256 cm2
Vậy cạnh hình vuông nhỏ = 15 vì 225 = 15 x 15
Cạnh hình vuông lớn = 16 vì 256 = 16 x 16
Đáp số : 15 cm, 16 cm