Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

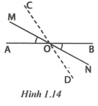
Theo đề bài ta có A O M ^ = M O C ^ , B O N ^ = D O N ^ mà A O M ^ = B O N ^ (hai góc đối đỉnh) nên M O C ^ = D O N ^ .
Ta có M O D ^ + D O N ^ = 180 ° (hai góc kề bù), suy ra M O D ^ + M O C ^ = 180 ° .
Hai góc MOD và MOC là hai góc kề, có tổng bằng 180 ° nên hai tia OC, OD đối nhau.
Chứng tỏ một tia là tia phân giác

Bài 1
x x' y y' O ) 1 2 3 4 m n
a
Ta có:
\(\widehat{O_1}=\widehat{O_2}=60^0\left(đ.đ\right)\)
\(\widehat{O_1}+\widehat{O_2}=180^0\Rightarrow\widehat{0_2}=180^0-\widehat{O_1}=180-60^0=120^0\)
\(\widehat{O_2}=\widehat{O_4}=120^0\left(đ.đ\right)\)
b
Ta có:
\(\widehat{x'Oy}=\widehat{y'Ox}\Rightarrow\frac{1}{2}\widehat{x'Oy}=\frac{1}{2}\widehat{y'Ox}\Rightarrow\widehat{yOn}=\widehat{xOm}\)
\(\widehat{x'Oy}+\widehat{yOx}=180^0\)
\(\Rightarrow2\cdot\widehat{yOn}+\widehat{yOx}=180^0\)
\(\Rightarrow\widehat{yOn}+\widehat{yOx}+\widehat{xOm}=180^0\)
\(\Rightarrowđpcm\)
Bài 2
A O B C D M
a
Ta có:
\(\widehat{BOD}=\widehat{AOC}=90^0\Rightarrow\widehat{BOC}+\widehat{COD}=\widehat{AOD}+\widehat{COD}\Rightarrow\widehat{BOC}=\widehat{AOD}\)
b
Ta có:
\(\widehat{BOM}=\widehat{BOC}+\widehat{COM}=\widehat{AOD}+\widehat{MOD}=\widehat{MOA}\)
Hiển nhiên OM nằm giữa \(\widehat{AOB}\) nên suy ra đpcm

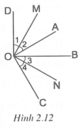
Ta có O C ⊥ O A ⇒ A O C ^ = 90 ° . O D ⊥ O B ⇒ B O D ^ = 90 ° .
Tia OB nằm giữa hai tia OA, OC.
Do đó A O B ^ + B O C ^ = 90 ° . (1)
Tương tự, ta có A O B ^ + A O D ^ = 90 ° . (2)
Từ (1) và (2) ⇒ B O C ^ = A O D ^ (cùng phụ với A O B ^ ).
Tia OM là tia phân giác của góc AOD ⇒ O 1 ^ = O 2 ^ = A O D ^ 2 .
Tia ON là tia phân giác của góc BOC ⇒ O 3 ^ = O 4 ^ = B O C ^ 2 .
Vì A O D ^ = B O C ^ nên O 1 ^ = O 2 ^ = O 3 ^ = O 4 ^ .
Ta có A O B ^ + B O C ^ = 90 ° ⇒ A O B ^ + O 3 ^ + O 4 ^ = 90 ° ⇒ A O B ^ + O 3 ^ + O 2 ^ = 90 ° .
Do đó M O N ^ = 90 ° ⇒ O M ⊥ O N