Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. * A(x) = \(-2x^2+3x-4x^3+\dfrac{3}{5}-5x^4\)
A(x)= \(-5x^4-4x^3-2x^2+3x+\dfrac{3}{5}\)
*B(x) = \(3x^4+\dfrac{1}{5}-7x^2+5x^3-9x\)
B(x)= \(3x^4+5x^3-7x^2-9x+\dfrac{1}{5}\)
A(x) +B(x) = \(-5x^4-4x^3-2x^2+3x+\dfrac{3}{5}+3x^4+5x^3-7x^2-9x+\dfrac{1}{5}\)
\(-\left(5x^4-3x^4\right)-\left(4x^3-5x^3\right)-\left(2x^2+7x^2\right)+\left(3x-9x\right)+\left(\dfrac{3}{5}+\dfrac{1}{5}\right)\)
\(=-2x^4+x^3-9x^2-6x+\dfrac{4}{5}\)
B(x)-A(x)=\(\left(3x^4+5x^3-7x^2-9x+\dfrac{1}{5}\right)-\left(5x^4-4x^3-2x^2+3x+\dfrac{3}{5}\right)\)
\(3x^4+5x^3-7x^2-9x+\dfrac{1}{5}-5x^4+4x^3+2x^2-3x-\dfrac{3}{5}\)
\(\left(3x^4-5x^4\right)+\left(5x^3+4x^3\right)-\left(7x^2-2x^2\right)-\left(9x+3x\right)+\left(\dfrac{1}{5}-\dfrac{3}{5}\right)\)
\(-2x^4+9x^3-5x^2-12x+\dfrac{2}{5}\)
Đúng 100% nha.Bạn Thanh bạn ấy tính nhầm và àm nhầm nên kq mới như vậy
Cho 2 đa thức sau: A(x)=-2x2+3x-4x3+\(\dfrac{3}{5}\)-5x4
B(x)=3x4+\(\dfrac{1}{5}\)-7x2+5x3-9x
a.sắp xếp các đa thức sau theo lũy thừa giảm dần của biến.
A(x)= -5x4 -4x3 -2x2 +3x+\(\dfrac{3}{5}\)
B(x)= 3x4 +5x3 -7x2 -9x+ \(\dfrac{1}{5}\)
b. A(x)+B(x)=(-5x4 -4x3 -2x2 +3x+\(\dfrac{3}{5}\))+ (3x4 +5x3 -7x2 -9x+\(\dfrac{1}{5}\) ) =-5x4 -4x3 -2x2 +3x+\(\dfrac{3}{5}\)+3x4 +5x3 -7x2 -9x +\(\dfrac{1}{5}\)
= (-5x4 +3x4 )+(-4x3 +5x3) +(-2x2 -7x2)+(3x-9x)+(\(\dfrac{3}{5}\)+\(\dfrac{1}{5}\))
= -2x4 +x3 -8x2 -6x+\(\dfrac{4}{5}\)
A(x)-B(x)=(-5x4 -4x3 -2x2 +3x+\(\dfrac{3}{5}\))-(3x4 +5x3 -7x2 -9x+\(\dfrac{1}{5}\) )
=-5x4 -4x3 -2x2 +3x+\(\dfrac{3}{5}\)-3x4 -5x3 +7x2 +9x-\(\dfrac{1}{5}\)
=(-5x4 -3x4 )+(-4x3-5x3) +(-2x2 +7x2)+(3x+9x)+(\(\dfrac{3}{5}\)-\(\dfrac{1}{5}\))
=-8x4-9x2+5x2+12x+\(\dfrac{2}{5}\)
CHÚC BN HỌC TỐT

Câu 1:
a) \(P\left(x\right)=x^5+7x^4-9x^3+\left(-3x^2+x^2\right)-\frac{1}{4}x\)
\(P\left(x\right)=x^5+7x^4-9x^3-2x^2-\frac{1}{4}x\)
\(Q\left(x\right)=-x^5+5x^4-2x^3+\left(x^2+3x^2\right)-\frac{1}{4}\)
\(Q\left(x\right)=-x^5+5x^4-2x^3+4x^2-\frac{1}{4}\)
b) \(P\left(x\right)+Q\left(x\right)=\left(x^5+7x^4-9x^3-2x^2-\frac{1}{4}x\right)+\left(-x^5+5x^4-2x^3+4x^2-\frac{1}{4}\right)\)
\(P\left(x\right)+Q\left(x\right)=x^5+7x^4-9x^3-2x^2-\frac{1}{4}x-x^5+5x^4-2x^3+4x^2-\frac{1}{4}\)
\(P\left(x\right)+Q\left(x\right)=\left(x^5-x^5\right)+\left(7x^4+5x^4\right)-\left(9x^3+2x^3\right)+\left(-2x^2+4x^2\right)-\frac{1}{4}x-\frac{1}{4}\)
\(P\left(x\right)+Q\left(x\right)=12x^4-11x^3+2x^2-\frac{1}{4}-\frac{1}{4}\)
\(P\left(x\right)-Q\left(x\right)=\left(x^5+7x^4-9x^3-2x^2-\frac{1}{4}x\right)-\left(-x^5+5x^4-2x^3+4x^2-\frac{1}{4}\right)\)
\(P\left(x\right)-Q\left(x\right)=x^5+7x^4-9x^3-2x^2-\frac{1}{4}x+x^5-5x^4+2x^3-4x^2+\frac{1}{4}\)
\(P\left(x\right)-Q\left(x\right)=\left(x^5+x^5\right)+\left(7x^4-5x^4\right)+\left(-9x^3+2x^3\right)-\left(2x^2+4x^2\right)-\frac{1}{4}x+\frac{1}{4}\)
\(P\left(x\right)-Q\left(x\right)=2x^5+2x^4-7x^3-6x^2-\frac{1}{4}x+\frac{1}{4}\)
c) \(P\left(x\right)=x^5+7x^4-9x^3-2x^2-\frac{1}{4}x\)
\(P\left(0\right)=0^5+7\cdot0^4-9\cdot0^3-2\cdot0^2-\frac{1}{4}\cdot0\)
\(P\left(0\right)=0\)
\(Q\left(x\right)=-x^5+5x^4-2x^3+4x^2-\frac{1}{4}\)
\(Q\left(0\right)=0^5+5\cdot0^4-2\cdot0^3+4\cdot0^2-\frac{1}{4}\)
\(Q\left(0\right)=-\frac{1}{4}\)
Vậy \(x=0\) là nghiệm của đa thức P(x) nhưng không là nghiệm của đa thức Q(x)

Ta có: P(x) = -5x3 - 1313 + 8x4 + x2 và Q(x) = x2 – 5x – 2x3 + x4 - 2323.
Ta sắp xếp hai đa thức theo lũy thừa giảm dần của biến như sau:
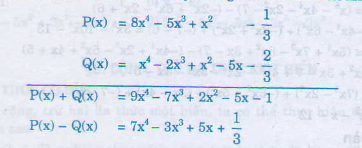 .
.
Ta có: P(x) = -5x3 – 1/3 + 8x4 + x2 và Q(x) = x2 – 5x – 2x3 + x4 – 2/3.
Ta sắp xếp hai đa thức theo lũy thừa giảm dần của biến như sau:


a) \(\frac{2}{3a}-\frac{3}{a}=\frac{2}{3a}-\frac{9}{3a}=\frac{-7}{3a}=\frac{7}{15}\Leftrightarrow-3a=15\Leftrightarrow a=-5\)
b)\(2x^3-1=15\Leftrightarrow2x^3=16\Leftrightarrow x^3=8\Leftrightarrow x=2\)
\(\Rightarrow\frac{2+16}{9}=\frac{y-15}{16}=2\Leftrightarrow y-15=32\Leftrightarrow y=47\)
c) \(\left|x\right|=3\Rightarrow\orbr{\begin{cases}x=-3\\x=3\end{cases}}\) rồi xét 2 trường hợp để tính A nhé :)
Bài 1: ĐK của a: \(a\ne0\)
Quy đồng VT ta có: \(\frac{2a-9a}{3a^2}=\frac{7}{15}\)
\(\Leftrightarrow\frac{-7a}{3a^2}=\frac{7}{15}\)
\(\Leftrightarrow-7a.15=3a^2.7\)
\(\Leftrightarrow-105a=21a^2\)
\(\Leftrightarrow-105a-21a^2=0\)
\(\Leftrightarrow a\left(-105-21a\right)=0\)
\(\Leftrightarrow\hept{\begin{cases}a=0\left(l\right)\\-105-21a=0\end{cases}\Leftrightarrow a=-5\left(n\right)}\)
Vậy:..

P(x)+Q(x)=(5x3-+7x4+8x2)+(8x2-5x-3x3+x4)
= 5x3-7x4+8x2+8x2-5x-3x3+x4
=(5x3-3x3)+(-7x4+x4)+(8x2+8x2)-5x
=2x3-6x4+16x2-5x
P(x)-Q(x)=(5x3-+7x4+8x2)-(8x2-5x-3x3+x4)
= 5x3-+7x4+8x2-8x2+5x+3x3-x4
=(5x3+3x3)+(-7x4_x4)+(8x2-8x2)+5x
= 8x3-8x4+5x
*Cách 1: Hàng ngang:
P(x) - Q(x) = (5x\(^3\) - \(\dfrac{1}{3}\) + 7x\(^4\) + 8x\(^2\)) - (8x\(^2\) - 5x - 3x\(^3\) + x\(^4\) - \(\dfrac{2}{3}\))
= 5x\(^3\) - \(\dfrac{1}{3}\) + 7x\(^4\) + 8x\(^2\) - 8x\(^2\) + 5x + 3x\(^3\) - x\(^4\) +\(\dfrac{2}{3}\)
= (5x\(^3\) + 3x\(^3\)) + (-\(\dfrac{1}{3}\) + \(\dfrac{2}{3}\)) + (7x\(^4\) - x\(^4\)) + (8x\(^2\) - 8x\(^2\)) + 5x
= 8x\(^3\) + \(\dfrac{1}{3}\) + 6x\(^4\) + 5x
Vậy P(x) - Q(x) = 8x\(^3\) + \(\dfrac{1}{3}\) + 6x\(^4\) + 5x
*Cách 2: Hàng dọc:
P(x) = 7x\(^4\) + 5x\(^3\) + 8x\(^2\) + 0x - \(\dfrac{1}{3}\)
-
Q(x) = x\(^4\) - 3x\(^3\) + 8x\(^2\) - 5x - \(\dfrac{2}{3}\)
Hay: P(x) = 7x\(^4\) + 5x\(^3\) + 8x\(^2\) + 0x - \(\dfrac{1}{3}\)
+
[-Q(x)] = -x\(^4\) + 3x\(^3\) - 8x\(^2\) + 5x + \(\dfrac{2}{3}\)
___________________________________________
P(x) - Q(x) = 6x\(^4\) + 8x\(^3\) + 5x - \(\dfrac{1}{3}\)
Vậy P(x) - Q(x) = 6x\(^4\) + 8x\(^3\) + 5x - \(\dfrac{1}{3}\)

1: \(\Leftrightarrow\left(x+1\right)^2=4\)
=>x+1=2 hoặc x+1=-2
=>x=1 hoặc x=-3
2: \(\Leftrightarrow7x-21=5x+25\)
=>2x=46
=>x=23
3: \(\Leftrightarrow x^2+4x+3=x^2+0.5x+4x+2\)
=>4,5x+2=4x+3
=>x=1

Bài 1:
Thay x=1 vào đa thức F(x) ta được:
F(1) = 14+2.13-2.12-6.1+5 = 0
=> x=1 là nghiệm của đa thức F(x)
Tương tự ta thế -1; 2; -2 vào đa thức F(x)
Vậy x=1 là nghiệm của đa thức F(x)

a: \(\dfrac{31-2x}{x+23}=\dfrac{9}{4}\)
=>121-8x=9x+207
=>-17x=86
hay x=-86/17
b: \(\dfrac{\left|2x-1\right|}{\dfrac{1}{2}}=\dfrac{18}{5}\)
=>|2x-1|=9/5
=>2x-1=9/5 hoặc 2x-1=-9/5
=>2x=14/5 hoặc 2x=-4/5
=>x=7/5 hoặc x=-2/5
\(P\left(x\right)+Q\left(x\right)=\left(-5x^3-\dfrac{1}{3}+8x^4+x^2\right)+\left(x^2-5x-2x^3+x^4-\dfrac{2}{3}\right)\)
\(=-5x^3-\dfrac{1}{3}+8x^4+x^2+x^2-5x-2x^3+x^4-\dfrac{2}{3}\)
\(=-5x+\left(x^2+x^2\right)+\left(-5x^3-2x^3\right)+\left(8x^4+x^4\right)+\left(-\dfrac{1}{3}-\dfrac{2}{3}\right)\)
\(=-5x+2x^2-7x^3+9x^4-1\)
\(P\left(x\right)-Q\left(x\right)=\left(-5x^3-\dfrac{1}{3}+8x^4+x^2\right)-\left(x^2-5x-2x^3+x^4-\dfrac{2}{3}\right)\)
\(=-5x^3-\dfrac{1}{3}+8x^4+x^2-x^2+5x+2x^3-x^4+\dfrac{2}{3}\)
\(=5x+\left(x^2-x^2\right)+\left(-5x^3+2x^3\right)+\left(8x^4-x^4\right)+\left(-\dfrac{1}{3}+\dfrac{2}{3}\right)\)
\(=5x-3x^3+7x^4+\dfrac{1}{3}\)
Ta có: \(P\left(x\right)+Q\left(x\right)=\left(-5x^3-\dfrac{1}{3}+8x^4+x^2\right)+\left(x^2-5x-2x^3+x^4-\dfrac{2}{3}\right)\)
\(=-5x^3-\dfrac{1}{3}+8x^4+x^2+x^2-5x-2x^3+x^4-\dfrac{2}{3}\)
\(=\left(-5x^3-2x^3\right)-\left(\dfrac{1}{3}+\dfrac{2}{3}\right)+\left(8x^4+x^4\right)+\left(x^2+x^2\right)-5x\)
\(=-7x^3+9x^4+2x^2-5x-1\)
Lại có: \(P\left(x\right)-Q\left(x\right)=\left(-5x^3-\dfrac{1}{3}+8x^4+x^2\right)-\left(x^2-5x-2x^3+x^4-\dfrac{2}{3}\right)\)
\(=-5x^3-\dfrac{1}{3}+8x^4+x^2-x^2+5x+2x^3-x^4+\dfrac{2}{3}\)
\(=\left(-5x^3+2x^3\right)+\left(8x^4-x^4\right)+\left(x^2-x^2\right)+5x-\left(\dfrac{1}{3}-\dfrac{2}{3}\right)\)
\(=-3x^3+7x^4+5x+\dfrac{1}{3}\)