Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

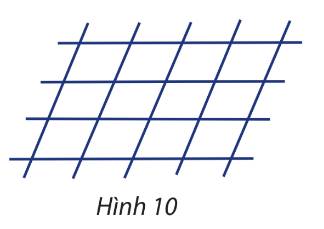
Ta thấy rằng, cứ 2 đường thẳng song song cắt 2 đường thẳng song song khác thì tạo thành một hình bình hành
Do đó, hình bình hành tạo thành được xác định qua 2 công đoạn
Công đoạn 1: Chọn 2 đường thẳng trong 4 đường nằm ngang, có:
\(C_4^2 = \frac{{4!}}{{2!.2!}} = 6\)
Công đoạn 2: Chọn 2 đường thẳng trong 5 đường xiên, có: \(C_4^2 = \frac{{5!}}{{2!.3!}} = 10\)
Vậy số hình bình hành được tạo thành là: \(6.10 = 60\) (hình bình hành)

Số cách chọn 2 đường thằng song song trong 6 đường thằng song song là: \(C_6^2\) (cách chọn)
Số cách chọn 2 đường thằng song song trong 8 đường thằng song song cùng vuông góc với 6 đường thằng song song ban đầu là: \(C_8^2\) (cách chọn)
Áp dụng quy tắc nhân, ta có số hình chữ nhật có thể tạo thành là: \(C_8^2.C_6^2 = 420\) ( hình chữ nhật)

A B C D O M N E F
a) Giả sử \(\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{OB}+\overrightarrow{OD}\)
\(\Leftrightarrow\overrightarrow{OA}+\overrightarrow{OC}-\overrightarrow{OB}-\overrightarrow{OD}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{OA}+\overrightarrow{BO}+\overrightarrow{OC}+\overrightarrow{DO}=\overrightarrow{0}\)
\(\Leftrightarrow\left(\overrightarrow{BO}+\overrightarrow{OA}\right)+\left(\overrightarrow{DO}+\overrightarrow{OC}\right)=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{BA}+\overrightarrow{DC}=\overrightarrow{0}\) (đúng do tứ giác ABCD là hình bình hành).
b) \(\overrightarrow{ME}+\overrightarrow{FN}=\overrightarrow{MA}+\overrightarrow{AE}+\overrightarrow{FC}+\overrightarrow{CN}\)
\(=\left(\overrightarrow{MA}+\overrightarrow{CN}\right)+\left(\overrightarrow{AE}+\overrightarrow{FC}\right)\).
Do các tứ giác AMOE, MOFB, OFCN, EOND cũng là các hình bình hành.
Vì vậy \(\overrightarrow{CN}=\overrightarrow{FO}=\overrightarrow{BM};\overrightarrow{FC}=\overrightarrow{ON}=\overrightarrow{ED}\).
Do đó: \(\overrightarrow{ME}+\overrightarrow{FN}=\left(\overrightarrow{MA}+\overrightarrow{CN}\right)+\left(\overrightarrow{AE}+\overrightarrow{FC}\right)\)
\(=\left(\overrightarrow{MA}+\overrightarrow{BM}\right)+\left(\overrightarrow{AE}+\overrightarrow{ED}\right)\)
\(=\overrightarrow{BA}+\overrightarrow{AD}=\overrightarrow{BD}\) (Đpcm).

Cách 1:
TH 1: Chọn 2 điểm thuộc đường thẳng có 4 điểm
Chọn 2 điểm từ đường thẳng trên có \(C_4^2\) cách
Chọn 1 điểm từ đường thẳng còn lại có 5 cách
=> Số tam giác tạo thành là \(5.C_4^2 = 30\)
TH 2: Chọn 2 điểm thuộc đường thẳng có 5 điểm
Chọn 2 điểm từ đường thẳng dưới có \(C_5^2\) cách
Chọn 1 điểm từ đường thẳng còn lại có 4 cách
=> Số tam giác tạo thành là \(4.C_5^2 = 40\)
Vậy có tất cả 70 tam giác được tạo thành.
Cách 2:
Số cách chọn 3 điểm bất kì là: \(C_9^3 = 84\) cách
Số cách chọn 3 điểm thẳng hàng là: \(C_4^3 +C_5^3 =14 \) cách
=> Số cách chọn 3 điểm không thẳng hàng là: 84 - 14 = 70 (cách)
Do đó ta có thể có 70 tam giác.

1). Tam giác ABF và tam giác ACE ần lượt cân tại F, E và
F B A ^ = E C A ^ = A ^ 2 ⇒ Δ A B F ∽ Δ A C E .
2). Giả sử G là giao điểm của BE và CF.
Ta có G F G C = B F C E = A B A C = D B D C ⇒ G D ∥ F B , và F B ∥ A D ta có G ∈ A D .
3). Chứng minh B Q G ^ = Q G A ^ = G A E ^ = G A C ^ + C A E ^ = G A B ^ + B A F ^ = G A F ^ , nên AGQF nội tiếp, và Q P G ^ = G C E ^ = G F Q ^ , suy ra tứ giác FQGP nội tiếp.
1) Chứng minh rằng tam giác \( A B F \) đồng dạng với tam giác \( A C E \):
- Tam giác \(ABF\) và \(ACE\) có:
+ Góc \(A\) chung.
+ Góc \(BAF\) bằng góc \(CAE\) (vì \(AD\) là phân giác của góc \(BAC\) và \(CF\), \(BE\) song song với \(AD\)).
Do đó, tam giác \(ABF\) đồng dạng với tam giác \(ACE\) (theo trường hợp góc-góc).
2) Chứng minh rằng các đường thẳng \(BE\), \(CF\), \(AD\) đồng quy:
- Gọi \(G\) là giao điểm của \(BE\) và \(CF\).
- \(AD\) là phân giác góc \(BAC\), và \(BE\), \(CF\) song song với \(AD\). Do đó, \(G\) cũng nằm trên phân giác \(AD\).
- Vậy \(BE\), \(CF\), \(AD\) đồng quy tại \(G\).
3) Chứng minh rằng các điểm \(A\), \(P\), \(G\), \(Q\), \(F\) cùng thuộc một đường tròn:
- Gọi đường tròn ngoại tiếp tam giác \(GEC\) là \(\omega\).
- \(QE\) cắt \(\omega\) tại \(P\) khác \(E\), vậy \(P\) nằm trên đường tròn \(\omega\).
- \(GQ\) song song với \(AE\), và \(AE\) là đường kính của \(\omega\) (vì \(E\) là trung điểm của \(AC\) và \(G\) nằm trên phân giác của \(BAC\)). Do đó, \(GQ\) là dây cung của \(\omega\).
- \(PF\) là tiếp tuyến của \(\omega\) tại \(P\) (vì \(QE\) là tiếp tuyến và \(PF\) là phần kéo dài của \(QE\)).
- Góc \(PGF\) bằng góc \(GAC\) (cùng chắn cung \(GC\) của \(\omega\)).
- \(AF\) là trung trực của \(AB\), nên \(ABF\) là tam giác cân tại \(A\). Do đó, góc \(AFB\) bằng góc \(ABF\).
- Góc \(ABF\) bằng góc \(GAC\) (do đồng dạng của tam giác \(ABF\) và \(ACE\)).
- Vậy, góc \(PGF\) bằng góc \(AFB\). Do đó, \(A\), \(P\), \(G\), \(Q\), \(F\) cùng thuộc một đường tròn.

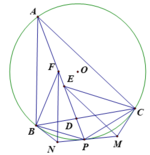
1). Gọi AD cắt (O) tại P khác A
Ta có P C M ^ = P A C ^ (góc tạo bởi tiếp tuyến và dây cung) = P E M ^ (góc đồng vị do E M ∥ A C );
Suy ra tứ giác ECMP nội tiếp. Từ đó suy ra M P C ^ = M E C ^ = E C A ^ = C A P ^ ⇒ PM tiếp xúc (O)
Tương tự PN tiếp xúc (O), suy ra MN tiếp xúc (O) tại P.


2) Theo 1). dễ thấy Δ B F A ∽ Δ B N P ⇒ Δ B N F ∽ Δ B P A ⇒ B N B P = F N A P (1).
Tương tự Δ C M E ∽ Δ C P A ⇒ C M C P = E M A P (2).
Từ (1) và (2), ta có B N C M ⋅ C P B P = F N E M và theo giả thiết F N E M = B N C M , suy ra C P = B P ⇒ A D là phân giác góc B A C ^ .

Câu 1: Tính chất hai đường thẳng song song là khi hai đường nó cắt một đường thẳng nào đó, sẽ tạo ra:
-Hai góc so le trong bằng nhau
-Hai góc đồng vị bằng nhau
-Hai góc trong cùng phía bù nhau
Câu 2: d được gọi là đường trung trực của AB khi d vuông góc với AB tại trung điểm của AB

Đáp án C
+Với m=1 ta có d: y=1 và d’: y=6
do đó hai đường thẳng này song song với nhau.
+ Với m =-1 ta có d: y= -2x-1 và d’: y= 6
suy ra hai đường thẳng này cắt nhau tại M(-7/2; 6)
+ Với m ≠ ± 1 khi đó hai đường thẳng trên là đồ thị của hàm số bậc nhất nên song song với nhau khi và chỉ khi:
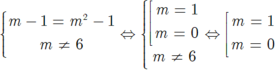
Đối chiếu với điều kiện m≠± 1 suy ra m= 0.
Vậy m= 0 và m= 1 là giá trị cần tìm.
Chọn C.
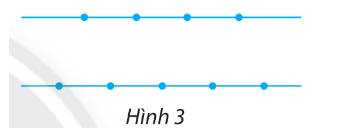
Số hình bình hành tạo thành là: \(C^2_{10}\cdot C^2_9=1620\left(đường\right)\)