Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do mạch chỉ có tụ C thì u vuông pha với i, nên ta có:
\(\left(\frac{u}{U_0}\right)^2+\left(\frac{i}{I_0}\right)^2=1\)
\(\Rightarrow\left(\frac{60}{U_0}\right)^2+\left(\frac{\sqrt{3}}{I_0}\right)^2=1\)
\(\left(\frac{60\sqrt{2}}{U_0}\right)^2+\left(\frac{\sqrt{2}}{I_0}\right)^2=1\)
\(\Rightarrow\begin{cases}U_0=120V\\I_0=2A\end{cases}\)

Ta có: \(W=W_t+W_d\)
\(\Leftrightarrow W_t=W_{dmax}-W_d\)
\(=\frac{1}{2}C.U^2_0-\frac{1}{2}Cu^2\)
\(=5.10^{-5}J\)

\(W=W_{Cmax}= W_L+W_C\)
\(=> W_L = W_{Cmax}-W_C= \frac{1}{2}C.(U_0^2-u^2)=3,96.10^{-4}J= 396\mu J.\)

Áp dụng công thức tính năng lượng điện từ trường ta có
W = Wđ = Wt \(\Rightarrow\frac{1}{2}LI_0^2=\frac{1}{2}lI^2+\frac{1}{2}Cu^2\)
\(\Rightarrow u=\sqrt{\left(I_0^2-I^2\right)\frac{L}{C}}\Rightarrow u=\)\(\sqrt{\frac{0,1}{10^{-5}}\left(0,05^2-0,02^2\right)}=4\left(V\right)\)
chọn A

Hiệu điện thế cực đại giữa hai bản tụ trong khung dao động bằng 6V6V, điện dung của tụ bằng 1μF1μF . Biết dao động điện từ trong khung năng lượng được bảo toàn, năng lượng từ trường cực đại tập trung ở cuộn cảm bằng
A.18.10-6 J.
B.0,9.10-6 J.
C.9.10-6 J.
D.1,8.10-6 J.

Đáp án C.
lúc đầu ta có :
UMB=2UR => ZMB=2R <=> ZC=\(\sqrt{3}\)R mà C=\(\frac{L}{R^2}\) => ZL=\(\frac{R}{\sqrt{3}}\)
lúc sau ta có Uc' max :
Zc'.ZL=R2+ \(Z^2_L\) => Zc'=\(\frac{4R}{\sqrt{3}}\)
\(\text{tanφ}=\frac{Z_L-Z_C}{R}\Rightarrow\tan\varphi=-\sqrt{3}\Rightarrow\varphi=-\frac{\pi}{3}\)
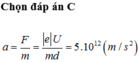
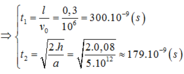
Đáp án: A
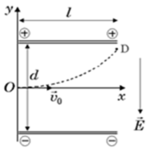
Phương trình chuyển động của electron trong điện trường là:
x = vot ; y = at2/2
=> Phương trình quỹ đạo là:
y = ax2 / (2vo2)
Hạt đi ra được khỏi tụ điện tại điểm D nên ta có:
x = vot = l; y = at2/2
=>t = l/vo = 0,05/ 106 = 50 ns