
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


câu này là có một người ghét lớp phó học tập nên mik mới đăng !

diện tích của hình tam giác là
\(\frac{\sqrt{3}\times2\sqrt{5}}{2}\approx3,87\)
đs: \(\approx3,87\)
vì theo tính chất của tam giác vuông là cạnh lớn nhất là cạnh huyền vậy ta lấy 2 cạnh còn lại nhân với nhau và chia cho 2

Bài 4:
Gọi 3 số là a,b,c
Ta có \(a:b=2:3\Rightarrow\dfrac{a}{2}=\dfrac{b}{3};a:c=4:9\Rightarrow\dfrac{a}{4}=\dfrac{c}{9}\)
\(\Rightarrow\dfrac{a}{4}=\dfrac{b}{6}=\dfrac{c}{9}\Rightarrow\dfrac{a^3}{64}=\dfrac{b^3}{216}=\dfrac{c^3}{729}\) và \(a^3+b^3+c^3=-1009\)
Áp dụng t/c dtsbn:
\(\dfrac{a^3}{64}=\dfrac{b^3}{216}=\dfrac{c^3}{729}=\dfrac{a^3+b^3+c^3}{64+216+729}=\dfrac{-1009}{1009}=-1\\ \Rightarrow\left\{{}\begin{matrix}a^3=-64\\b^3=-216\\c^3=-729\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=-4\\b=-6\\c=-9\end{matrix}\right.\)
Vậy ...
Bài 5:
Gọi số sách tủ 1,2,3 trước khi chuyển là là a,b,c (cuốn;a,b,c∈N*)
Ta có \(\left(a-100\right):b:\left(c+100\right)=16:15:14\Rightarrow\dfrac{a-100}{16}=\dfrac{b}{15}=\dfrac{c+100}{14}\)
Và \(a+b+c=2250\)
Áp dụng t.c dstbn:
\(\dfrac{a-100}{16}=\dfrac{b}{15}=\dfrac{c+100}{14}=\dfrac{a-100+b+c+100}{16+15+14}=\dfrac{2250}{45}=50\\ \Rightarrow\left\{{}\begin{matrix}a-100=800\\b=750\\c+100=700\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=900\\b=750\\c=600\end{matrix}\right.\)
Vậy...


Câu 3:
\(\widehat{A}=\widehat{B}=\widehat{C}=60^0\)

a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x-1}{2}=\dfrac{y-2}{3}=\dfrac{z-3}{4}=\dfrac{x-2y+3z-1+4-9}{2-2\cdot3+3\cdot4}=1\)
Do đó: x=3; y=5; z=7

a: ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC^2=6^2+8^2=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
Xét ΔABC có AB<AC<BC
mà \(\widehat{ACB};\widehat{ABC};\widehat{BAC}\) lần lượt là các góc đối diện của các cạnh AB,AC,BC
nên \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)
b: Xét ΔBAK vuông tại A và ΔBHK vuông tại H có
BK chung
\(\widehat{ABK}=\widehat{HBK}\)
Do đó: ΔBAK=ΔBHK
c: Ta có: ΔBAK=ΔBHK
=>KA=KH
Xét ΔKAI vuông tại A và ΔKHC vuông tại H có
KA=KH
AI=HC
Do đó: ΔKAI=ΔKHC
=>\(\widehat{AKI}=\widehat{HKC}\)
mà \(\widehat{HKC}+\widehat{AKH}=180^0\)(hai góc kề bù)
nên \(\widehat{AKH}+\widehat{AKI}=180^0\)
=>H,K,I thẳng hàng
d: Xét ΔBIC có \(\dfrac{BA}{AI}=\dfrac{BH}{HC}\)
nên AH//IC

Đúng rồi bạn, tất cả lý thuyết đều ở trong sách giáo khoa đấy.
@Cỏ
#Forever

Ta có P(x)=x^2+2x+x+2+3
=x(2+x)+x+2+3
=(x+2)^2+3
Mà (x+2)^2>=0=>P(x)>0
=> P(x) vô nghiệm



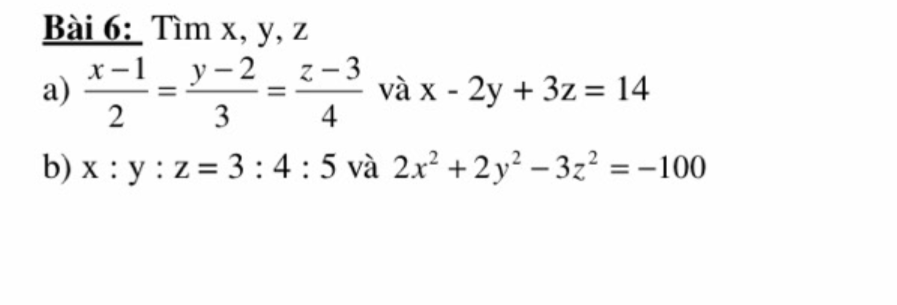
 NHỚ LÀM THEO KIẾN THỨC LỚP 7 NHA!! CẢM ƠN Ạ!
NHỚ LÀM THEO KIẾN THỨC LỚP 7 NHA!! CẢM ƠN Ạ!