Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Ta có: O A O B = F 2 F 1 =3 , OA + OB = 20 cm
⟹ OA = 15 cm; F = F1 + F2 = 20 N.

Chọn B.
Để đòn bẩy cân bằng như ban đầu thì: PA.OA = PB.OB
![]()

Đáp án C

m1 = 2M, m2 = M
Để khối tâm của hệ tại trung điểm AB (GA =GB) thì:
m1. AG = m2. GB + m3 GC
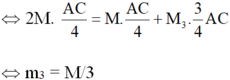

Chọn A.
Ta có:
F = k . Δ l ⇒ Δ l = F k
Hai lò xo dãn như nhau, nên: Δ l 1 = Δ l 2
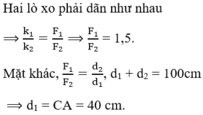

Chọn C
Lực căng bề mặt tác dụng lên mặt trong và mặt ngoài của vòng nhôm.
F c = 2 σ πd = 2 . 72 . 10 - 3 . π . 0 , 2 = 0 , 09 N

Chọn C.
Khi buộc đầu dưới vật khối lượng m1, lò xo dãn:
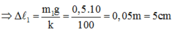
Khi buộc vào điểm giữa của lò xo một vật nặng thứ hai, thì nửa trên của lò xo có độ cứng k’. Vì độ cứng k của lò xo tỷ lệ nghịch với chiều dài ℓ nên
![]()
Khi buộc vào chính giữa lò xo vật m2 nửa trên dãn thêm:
![]()
⟹ Chiều dài lò xo lúc này là:
![]()

a) Vị trí lực đàn hồi cân bằng với trọng lực:
kx0 = mg => x0 = 0,02 m = 2 cm.
b) Vận tốc của vật tại vị trí lực đàn hồi cân bằng với trọng lực:
1/2 . k(xo)2 = ½k(vcb)2 => |vcb| = 0,2√5 m/s = 20√5 (cm/s).
a. Ở vị trí cân bằng thì lực đàn hồi cân bằng với trọng lượng
\(\Rightarrow F_{đh}=P\Rightarrow k.\Delta l_0=mg\)
\(\Rightarrow \Delta l_0=\dfrac{mg}{k}=\dfrac{0,4.10}{200}=0,02m=2cm\)
b. Vị trí đó chính là vị trí cân bằng.
Chọn gốc thế năng ở vị trí cân bằng.
Thả vật ở vị trí lò xo không giãn \(\Rightarrow x_1=2cm\)
Áp dụng định luật bảo toàn cơ năng ta có:
\(\dfrac{1}{2}.k.x_1^2=\dfrac{1}{2}.m.v^2\)
\(\Rightarrow v = x_1.\sqrt{\dfrac{k}{m}}=2.\sqrt{\dfrac{200}{0,4}}==20\sqrt 5 (cm/s)\)
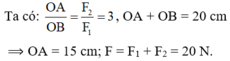
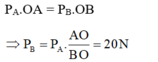

Chọn C.
Các phân tử khí lí tưởng luôn có khối lượng nên không thể bỏ qua được.