Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nó chỉ đúng khi A, B nằm trong cùng một mặt phẳng góc phần tư thứ nhất hoặc ba thôi.
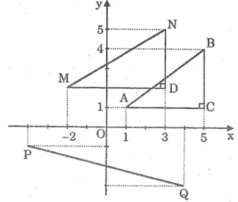
Chẳng hạn ở hình này, dễ thấy rằng MN là đường trung bình của hình thang ABDC(AC//BD) \(\Rightarrow MN=\frac{AC+BD}{2}\)
Lại có \(MN=y_M;AC=y_A;BD=y_B\)(vì trong trường hợp này tung độ của các điểm đều dương)
\(\Rightarrow y_M=\frac{y_A+y_B}{2}\)(đpcm thứ 1)
Tương tự, ta cũng có \(x_M=\frac{x_1+x_2}{2}\)(MP là đường trung bình của hình thang ABFE)
Nếu A, B nằm trong cùng một mặt phẳng góc phần tư thứ hai hoặc bốn thì:
Nếu như này thì cũng như trường hợp trên, ta chứng minh \(x_M=\frac{x_A+x_B}{2}\)một cách dễ dàng (MP là đường trung bình của hình thang ABFE(AE//BF))
Nhưng còn về y thì nó hơi khác một chút:
Dễ thấy \(MN=\frac{AC+BD}{2}\)
Vì tất cả các tung độ trong trường hợp này đều âm nên ta có \(-y_M=\frac{-y_A-y_B}{2}\)rốt cuộc vẫn có \(y_M=\frac{y_A+y_B}{2}\)
Còn trường hợp 2 điểm A, B nằm trên 2 góc phần tư khác nhau thì mình đang nghĩ.
Ý bạn là công thức \(x_M=\frac{x_A+x_B}{2}\)và \(y_M=\frac{y_A+y_B}{2}\)nếu M là trung điểm của AB đúng không?

a) Vì A, B thuộc (P) nên:
x A = − 1 ⇒ y A = 1 2 ⋅ - 1 2 = 1 2 x B = 2 ⇒ y B = 1 2 ⋅ 2 2 = 2 ⇒ A − 1 ; 1 2 , B ( 2 ; 2 )
b) Gọi phương trình đường thẳng (d) là y = ax + b.
Ta có hệ phương trình:
− a + b = 1 2 2 a + b = 2 ⇔ 3 a = 3 2 2 a + b = 2 ⇔ a = 1 2 b = 1
Vậy (d): y = 1 2 x + 1 .
c) (d) cắt trục Oy tại điểm C(0; 1) và cắt trục Ox tại điểm D(– 2; 0)
=> OC = 1 và OD = 2
Gọi h là khoảng cách từ O tới (d).
Áp dụng hệ thức về cạnh và đường cao vào ∆ vuông OCD, ta có:
1 h 2 = 1 O C 2 + 1 O D 2 = 1 1 2 + 1 2 2 = 5 4 ⇒ h = 2 5 5
Vậy khoảng cách từ gốc O tới (d) là 2 5 5 .

PTHĐGĐ là;
x^2-2mx-3+2m=0
Δ=(-2m)^2-4(2m-3)
=4m^2-8m+12
=4m^2-8m+4+8
=(2m-2)^2+8>0
=>(P) luôn cắt (d) tại hai điểm phân biệt
x1^2+x2^2=14
=>(x1+x2)^2-2x1x2=14
=>(2m)^2-2(2m-3)=14
=>4m^2-4m+6-14=0
=>4m^2-4m-8=0
=>m^2-m-2=0
=>(m-2)(m+1)=0
=>m=2 hoặc m=-1