
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\Rightarrow\dfrac{5}{4}-\dfrac{1}{4}x=\dfrac{3}{10}x-\dfrac{2}{5}\)
\(\Rightarrow\dfrac{5}{4}+\dfrac{2}{5}=\dfrac{3}{10}x-\dfrac{1}{4}x\)
\(\Rightarrow\dfrac{33}{20}=\dfrac{11}{20}x\)
\(\Rightarrow x=\dfrac{33}{20}\div\dfrac{11}{20}\)
\(\Rightarrow x=3\)
\(1\dfrac{1}{4}-x\dfrac{1}{4}=x\cdot30\%\cdot\dfrac{2}{5}\)
\(\Leftrightarrow\dfrac{5}{4}-x\dfrac{1}{4}=x\cdot\dfrac{3}{10}-\dfrac{2}{5}\)
\(\Leftrightarrow\dfrac{5}{4}-\dfrac{1}{4}x=\dfrac{3}{10}x-\dfrac{2}{5}\)
\(\Leftrightarrow25-5x=6x-8\)
\(\Leftrightarrow-5x-6x=-8-25\)
\(\Leftrightarrow-11x=-33\)
\(\Leftrightarrow x=3\)
Vậy x = 3

Cho 3 điểm k thẳng hàng A , B, C . Vẽ các đoạn thẳng AB, BC , CA. Vẽ đường thẳng a cắt AC , BC tương ứng tại D , E
đề 1: vẽ 3 đoạn thẳng sao cho mỗi đoạn thẳng cắt hai đoạn thẳng cobf lại tại đầu mút của chúng, rồi vẽ đường thẳng a cắt hai đoạn trong 3 đoạn thẳng đó. Đặt tên cho các giao điểm.
đề 2: cho 3 điểm không thẳng hàng A, B, C . Vẽ các đoạn thẳng AB, BC, CA. Vẽ đường thẳng a cắt AC và BC tương ứng tại D và E


Từ đề bài ta có:
\(T=\dfrac{1+2}{2}.\dfrac{1+3}{3}.\dfrac{1+4}{4}...\dfrac{1+98}{98}.\dfrac{1+99}{99}\)
\(=\dfrac{3}{2}.\dfrac{4}{3}.\dfrac{5}{4}...\dfrac{99}{98}.\dfrac{100}{99}\)
\(=\dfrac{100}{2}\)
\(=50\).
\(T=\left(\dfrac{1}{2}+1\right)\left(\dfrac{1}{3}+1\right)\left(\dfrac{1}{4}+1\right)...\left(\dfrac{1}{98}+1\right)\left(\dfrac{1}{99}+1\right)\)
\(T=\dfrac{3}{2}.\dfrac{4}{3}.\dfrac{5}{4}....\dfrac{99}{98}.\dfrac{100}{99}\)
\(T=\dfrac{3.4.5......99}{3.4.5......99}.\dfrac{100}{2}\)
\(T=50\)


a, \((\dfrac{-1}{2})\)2 -\(\dfrac{5}{6}\).\((\dfrac{-6}{7})-\dfrac{3}{4}:1\dfrac{2}{3}\)
=\(\dfrac{1}{4}+\dfrac{5}{7}-\dfrac{9}{20}\)
=\(\dfrac{35}{140}+\dfrac{100}{140}-\dfrac{63}{140}\)
=\(\dfrac{72}{140}\)= \(\dfrac{18}{35}\)

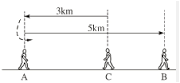
Một người đi từ C đến A rồi quay trở lại B (hình 49).
Ta qui ước chiều từ C đến B là chiều dương (nghĩa là quãng đường đi từ C về phía B được biểu thị bằng số dương và theo chiều ngược lại là số âm).
Tính quãng đường CB biết khoảng cách giữa C và A là 3km, khoảng cách giữa A và B là 5km
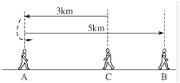
Một người đi từ C đến A rồi quay trở lại B (hình 49).
Ta qui ước chiều từ C đến B là chiều dương (nghĩa là quãng đường đi từ C về phía B được biểu thị bằng số dương và theo chiều ngược lại là số âm).
Tính quãng đường CB biết khoảng cách giữa C và A là 3km, khoảng cách giữa A và B là 5km.


Có thể đặt một bài toán như sau:
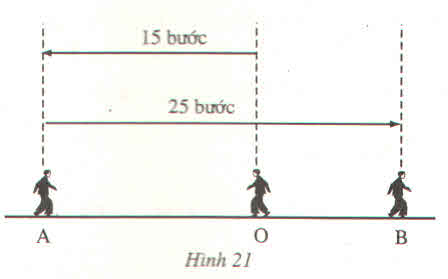
Một người bước từ O về phía A 15 bước rồi quay lại bước về phía B 25 bước. Hỏi người đó cách điểm đứng ban đầu O bao nhiêu bước?
A B O 15 bước 25 bước
Một người bước từ O về phía A 15 bước rồi quay lại bước về phía B 25 bước. Hỏi người đó cách điểm đứng ban đầu O bao nhiêu bước ?
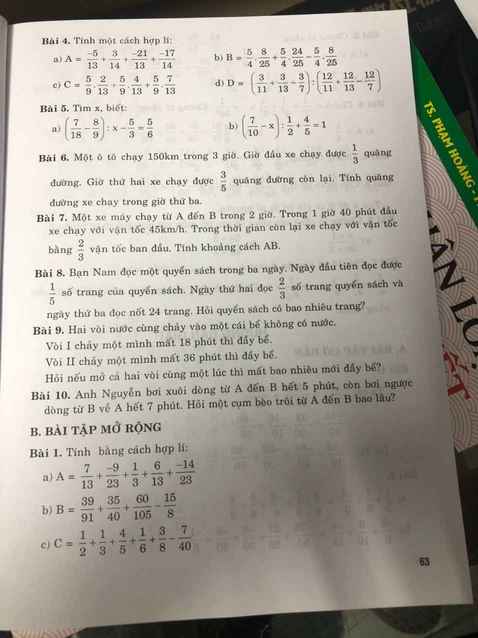




 giải giùm tớ nha
giải giùm tớ nha

 c
c
Bài 8:
Quyển sách đó có:
\(24:\left(1-\dfrac{1}{5}-\dfrac{2}{3}\right)=180\left(trang\right)\)
Bài 4:
a: \(A=\left(\dfrac{-5}{13}-\dfrac{21}{13}\right)+\left(\dfrac{3}{14}-\dfrac{17}{14}\right)=-2-1=-3\)
b: \(B=\dfrac{5}{4}\left(\dfrac{8}{25}+\dfrac{24}{25}-\dfrac{8}{25}\right)=\dfrac{5}{4}\cdot\dfrac{24}{25}=\dfrac{6}{5}\)
c: \(C=\dfrac{5}{9}\left(\dfrac{2}{13}+\dfrac{4}{13}+\dfrac{7}{13}\right)=\dfrac{5}{9}\cdot1=\dfrac{5}{9}\)
chị giúp em câu đ bài 4 với