Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng công thức (5.1 và 5.2 - SGK) ta tìm được:
A = 2,3 cm và φ = 0,73π
Phương trình dao động tổng hợp là: x = 2,3cos(5πt + 0,73π) (cm).

\(Z_L=100\Omega\)
\(Z_C=40\Omega\)
Theo giả thiết ta có:
\(R_1.R_2=(Z_L-Z_C)^2=60^2\)
\(R_1+R_2=\dfrac{U^2}{P}\)
\(\tan\varphi_1=\dfrac{60}{R_1}\)
\(\tan\varphi_2=\dfrac{60}{R_2}\)
Có: \(\varphi_1=2.\varphi_2\Rightarrow \tan \varphi_1=\tan 2\varphi_2=\dfrac{2\tan\varphi_2}{1-\tan^2\varphi_2}=\dfrac{60}{R_1}\)
\(\Rightarrow \dfrac{2\dfrac{60}{R_2}}{1-(\dfrac{60}{R_2})^2}=\dfrac{60}{R_1}\)
Biến đổi ta tìm đc \(R_2=60\sqrt 3\); \(R_1=20\sqrt 3\)
\(\Rightarrow P=\dfrac{U^2}{R_1+R_2}=60\sqrt 3(W)\)

Pha ban đầu của dao động tổng hợp được xác định bằng biểu thức
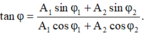
Đáp án B

Đáp án B
+ Pha ban đầu của dao động tổng hợp được xác định bằng biểu thức
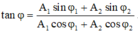


Đáp án C
Độ lệch pha giữa hai dao động được tính theo công thức
tan φ = A 1 sin φ 1 + A 2 sin φ 2 A 1 cos φ 1 + A 2 cos φ 2