Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

GIẢI THÍCH: Suất điện động xuất hiện trong các cuộn dây có dạng:
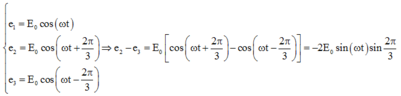
Theo giả thuyết của bài toán
![]()
Kết hợp với
![]()
Chọn C.

Nhiệt lượng
\(Q=I^2Rt=\frac{E^2_0t}{2R}=\frac{\left(\omega NBS\right)^2t}{2R}=\frac{\left(200.100\pi.0,002\right)^2.60}{2.1000}\)\(=474J\)

Vì \(T_0< T_1\) , nên E hướng xuống.
Lại có: \(T_1=2T_0\Leftrightarrow2\pi\sqrt{\frac{l}{g-a}}=2.2\pi\sqrt{\frac{l}{g}}\Rightarrow4a=3g\Leftrightarrow a=\frac{3}{4}g\)\(=7,5\left(m/s^2\right)\)
\(a=\frac{qE}{m}\Rightarrow E=\frac{ma}{q}=3,75.10^3\left(V/m\right)\)
Đáp án D

Suất điện động cảm ứng trong khung: \(e=-\phi'_{(t)}\)
\(\Rightarrow e=14,4.\sin(720t+\dfrac{\pi}{6})(V)\)

Tần số góc là:
\(w=\frac{720.2\pi}{60}=25\pi\)
Suất điện động cực đại là:
\(\Rightarrow E_0=N.B.S.w=200\frac{25.10^{-3}}{\pi}.4=500V\)
Suất điện động hiệu dụng là:
\(E=\frac{E_0}{\sqrt{2}}=250\sqrt{2V}\)

Tần số: f = 120 / 60 = 2Hz
Suy ra \(\omega=2\pi f=4\pi\)(rad/s)
Suất điện động cực đại: \(E_0=\omega NBS=4\pi.100.0,2.600.10^{-4}=4,8\pi\)(V)
Gốc thời gian lúc véc tơ pháp tuyến của mặt phẳng khung dây ngược hướng véc tơ cảm ứng từ -->\(\varphi=\pi\)(theo hàm sin)
Vậy PT suất điện động cảm ứng: \(E=4,8\pi\sin\left(4\pi t+\pi\right)\)(V)

Áp dụng công thức tính năng lượng điện từ trường ta có
W = Wđ = Wt \(\Rightarrow\frac{1}{2}LI_0^2=\frac{1}{2}lI^2+\frac{1}{2}Cu^2\)
\(\Rightarrow u=\sqrt{\left(I_0^2-I^2\right)\frac{L}{C}}\Rightarrow u=\)\(\sqrt{\frac{0,1}{10^{-5}}\left(0,05^2-0,02^2\right)}=4\left(V\right)\)
chọn A

GIẢI THÍCH:
Chọn B.