Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Vì LCω2 = 2 => ZC = 2ZL
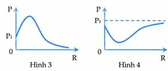
Xét đồ thị (2): 
 (1)
(1)
Khi R = 20Ω:  (2)
(2)
Từ (1) và (2) => ZC = 60Ω
Xét đồ thị (1): Khi R = 0:  (3)
(3)
Từ (1) và (3) tìm được r = 180Ω.

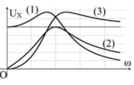
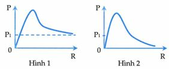
GIẢI THÍCH: (2) là đồ thị uR theo ω có đỉnh cộng hưởng
(1) là đồ thị của uc theo ω; (3) là đồ thị của uL theo ω.
Chọn A.

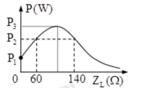
- Từ đồ thị ta thấy có hai giá trị của ZL là 60Ω và 140Ω cùng cho 1 giá trị P.
- Vị trí P3 đạt cực đại ứng với trường hợp cộng hưởng điện ZL = ZC
- Và có mối quan hệ giữa ZL3 với ZL1 và ZL2 là:
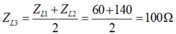
- Khi ZL = 0 thì mạch có công suất P1 thỏa mãn P3 /P1 = 3. Ta có:
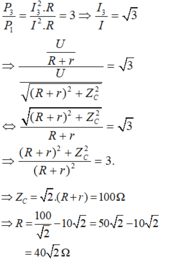

\(U_{RC}=const=U\) khi \(Z_{L1}=2Z_C=R\)
Mặt khác L thay đổi để : \(U_{Lmax}:U_{Lmax}=\frac{U\sqrt{R^2+Z^2_C}}{R}=\frac{U\sqrt{2^2+1}}{2}=\frac{U\sqrt{5}}{2}\)
\(\Rightarrow chọn.D\)
+,có C=C1=>U_R=\frac{U.R}{\sqrt{R^2+(Zl-ZC1)^2}}
+,U R ko đổi =>Zl=ZC1
+,có c=C1/2=>ZC=2ZC1
=>U(AN)=U(RL)=\frac{U\sqrt{r^2+Z^2l}}{\sqrt{R^2+(Zl-2Z^2C1)}}=u=200V

Chọn đáp án D
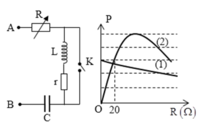
Phương pháp: Sử dụng bất đẳng thức Cosi để đánh giá giá trị của P.
Ta luôn có
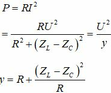
Theo bất đẳng thức Cosi ta có:
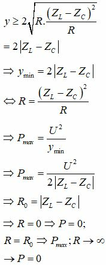

Đáp án D
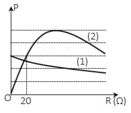
Phương pháp: Sử dụng bất đẳng thức Cosi để đánh giá giá trị của P
Ta luôn có:
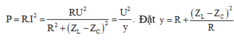
Theo bất đẳng thức Cosi ta có:
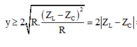
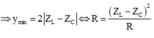
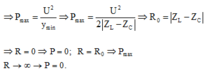
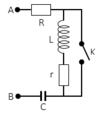

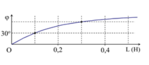
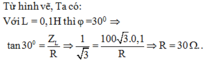
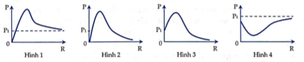
GIẢI THÍCH:
Chọn A.