Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do SAB là tam giác đều \(\Rightarrow SH\perp AB\)
Mà \(\left\{{}\begin{matrix}\left(SAB\right)\perp\left(ABCD\right)\\AB=\left(SAB\right)\cap\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow SH\perp\left(ABCD\right)\)
Gọi E là trung điểm CD, từ H kẻ \(HF\perp SE\) (F thuộc SE)
\(\left\{{}\begin{matrix}HE\perp CD\\SH\perp\left(ABCD\right)\Rightarrow SH\perp CD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SHE\right)\)
\(\Rightarrow CD\perp HF\)
\(\Rightarrow HF\perp\left(SCD\right)\Rightarrow HF=d\left(H;\left(SCD\right)\right)\)
\(HE=BC=a\) ; \(SH=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều cạnh a)
Hệ thức lượng:
\(HF=\dfrac{SH.HE}{\sqrt{SH^2+HE^2}}=\dfrac{a\sqrt{21}}{7}\)

Bạn kiểm tra lại đề,
1. ABCD là hình thang vuông tại A và B hay A và D? Theo dữ liệu này thì ko thể vuông tại B được (cạnh huyền DC nhỏ hơn cạnh góc vuông AB là cực kì vô lý)
2. SC và AC cắt nhau tại C nên giữa chúng không có khoảng cách. (khoảng cách bằng 0)
Nguyễn Việt Lâm
e xin loi a
ABCD là hình thang vuông tại A và D
còn đoạn sau khoảng cách giữa 2 đt SC và AC thì e kh biet no sai o đau
anh giup em vs ah

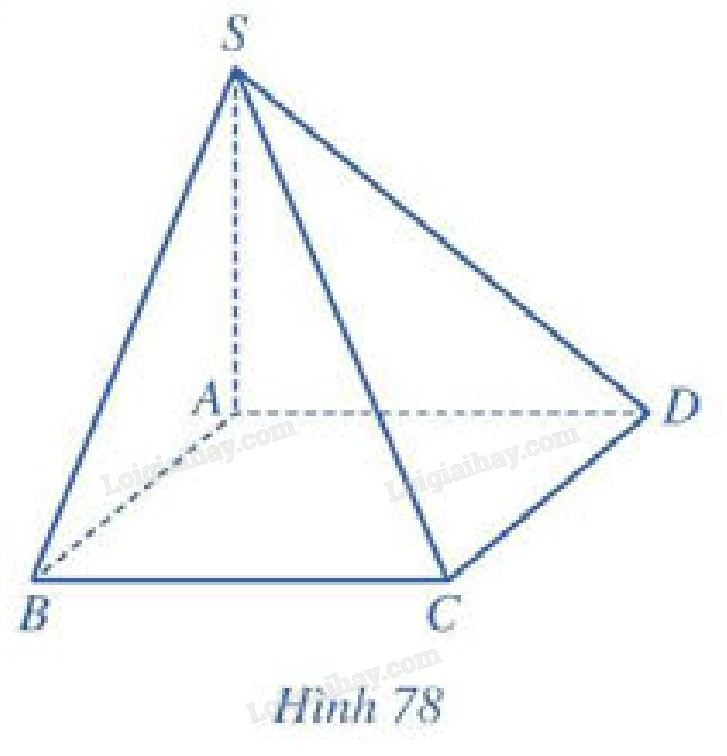
a) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot C{\rm{D}}\)
\(ABCD\) là hình vuông \( \Rightarrow A{\rm{D}} \bot C{\rm{D}}\)
\(\begin{array}{l} \Rightarrow C{\rm{D}} \bot \left( {SA{\rm{D}}} \right) \Rightarrow C{\rm{D}} \bot S{\rm{D}}\\ \Rightarrow d\left( {S,C{\rm{D}}} \right) = S{\rm{D}} = \sqrt {S{A^2} + A{{\rm{D}}^2}} = a\sqrt 2 \end{array}\)
b) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot A{\rm{D}}\)
\(ABCD\) là hình vuông \( \Rightarrow A{\rm{B}} \bot A{\rm{D}}\)
\( \Rightarrow A{\rm{D}} \bot \left( {SA{\rm{B}}} \right) \Rightarrow d\left( {D,\left( {SAB} \right)} \right) = A{\rm{D}} = a\)
c) Kẻ \(AH \bot S{\rm{D}}\left( {H \in S{\rm{D}}} \right)\).
\(C{\rm{D}} \bot \left( {SA{\rm{D}}} \right) \Rightarrow C{\rm{D}} \bot AH\)
\( \Rightarrow AH \bot \left( {SC{\rm{D}}} \right) \Rightarrow d\left( {A,\left( {SC{\rm{D}}} \right)} \right) = AH\)
Tam giác \(SAD\) vuông tại \(A\) có đường cao \(AH\)
\( \Rightarrow AH = \frac{{SA.A{\rm{D}}}}{{S{\rm{D}}}} = \frac{{a\sqrt 2 }}{2}\)
Vậy \(d\left( {A,\left( {SC{\rm{D}}} \right)} \right) = \frac{{a\sqrt 2 }}{2}\).

a.
Gọi H là trung điểm AB \(\Rightarrow SH\perp AB\Rightarrow SH\perp\left(ABCD\right)\) \(\Rightarrow SH\perp CD\)
Gọi E là trung điểm CD \(\Rightarrow HE||BC\Rightarrow HE\perp CD\)
\(\Rightarrow CD\perp\left(SHE\right)\)
Từ H kẻ \(HF\perp SE\)
\(\Rightarrow HF\perp\left(SCD\right)\Rightarrow HF=d\left(H;\left(SCD\right)\right)\)
\(SH=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều cạnh a), \(HE=BC=a\)
Hệ thức lượng: \(HF=\dfrac{SH.HE}{\sqrt{SH^2+HE^2}}=\dfrac{a\sqrt{21}}{7}\)
Do \(AH||CD\Rightarrow AH||\left(SCD\right)\Rightarrow d\left(A;\left(SCD\right)\right)=d\left(H;\left(SCD\right)\right)=\dfrac{a\sqrt{21}}{7}\)
b.
Theo tính chất trọng tâm, ta có \(GS=\dfrac{2}{3}HS\)
Mà \(HG\cap\left(SCD\right)=S\Rightarrow d\left(G;\left(SCD\right)\right)=\dfrac{2}{3}d\left(H;\left(SCD\right)\right)=\dfrac{2a\sqrt{21}}{21}\)
c.
Từ H kẻ \(HK\perp SA\)
Do \(\left\{{}\begin{matrix}SH\perp\left(ABCD\right)\Rightarrow SH\perp AD\\AD\perp AB\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\)
\(\Rightarrow AD\perp HK\)
\(\Rightarrow HK\perp\left(SAD\right)\Rightarrow HK=d\left(H;\left(SAD\right)\right)\)
Hệ thức lượng: \(HK=\dfrac{SH.AH}{\sqrt{SH^2+AH^2}}=\dfrac{a\sqrt{3}}{4}\)
Do \(BC||AD\Rightarrow BC||\left(SAD\right)\Rightarrow d\left(BC;SD\right)=d\left(BC;\left(SAD\right)\right)=d\left(B;\left(SAD\right)\right)\)
Mà \(\left\{{}\begin{matrix}BH\cap\left(SAD\right)=A\\BA=2HA\end{matrix}\right.\)
\(\Rightarrow d\left(BC;SD\right)=d\left(B;\left(SAD\right)\right)=2d\left(H;\left(SAD\right)\right)=\dfrac{a\sqrt{3}}{2}\)

a: AC vuông góc BD
AC vuông góc SD
=>AC vuông góc (SBD)
b: AD vuông góc AB
AB vuông góc SD
=>AB vuông góc (ADS)
=>(SAD) vuông góc (SAB)


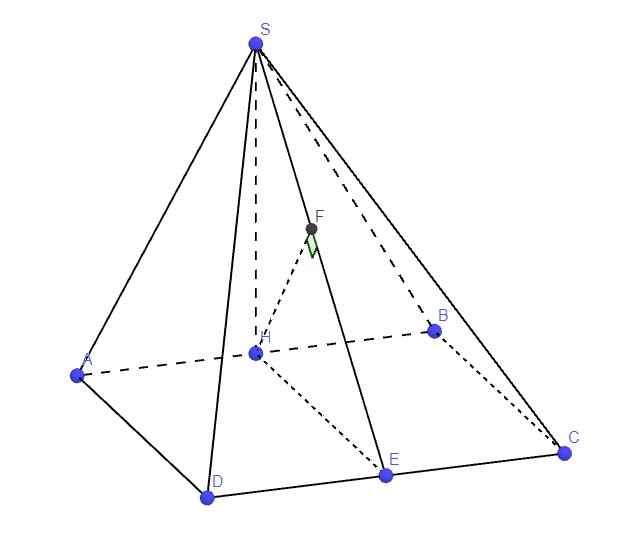
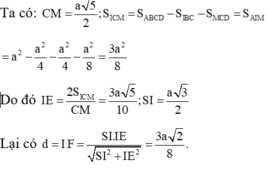
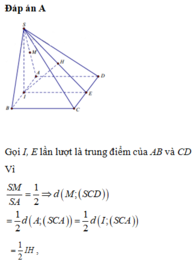

3.1. Xác định tọa độ điểm \(S\) và các điểm đã cho
\(\mathbf{n}_{\textrm{ } S A B} = \left(\right. 0 , \textrm{ } 1 , \textrm{ } 0 \left.\right) .\)
\(S = \left(\right. x , \textrm{ } y , \textrm{ } z \left.\right) , y = 0 , S A^{2} = x^{2} + 0^{2} + z^{2} = a^{2} , S B^{2} = \left(\right. x - a \left.\right)^{2} + 0^{2} + z^{2} = a^{2} .\)
Từ \(S A^{2} = S B^{2}\) ta có
\(x^{2} + z^{2} = \left(\right. x - a \left.\right)^{2} + z^{2} \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } x^{2} = x^{2} - 2 a x + a^{2} \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } - 2 a x + a^{2} = 0 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } x = \frac{a}{2} .\)
Thay vào \(x^{2} + z^{2} = a^{2}\):
\(\left(\right. \frac{a}{2} \left.\right)^{2} + z^{2} = a^{2} \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } z^{2} = a^{2} - \frac{a^{2}}{4} = \frac{3 a^{2}}{4} \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } z = \pm \frac{\sqrt{3} \textrm{ } a}{2} .\)
Thông thường ta chọn \(z > 0\). Vậy
\(\boxed{S = \left(\right. \frac{a}{2} , \textrm{ }\textrm{ } 0 , \textrm{ }\textrm{ } \frac{\sqrt{3} \textrm{ } a}{2} \left.\right) .}\)
\(I = \left(\right. \frac{0 + a}{2} , \textrm{ } \frac{0 + 0}{2} , \textrm{ } 0 \left.\right) = \left(\right. \frac{a}{2} , \textrm{ } 0 , \textrm{ } 0 \left.\right) .\)
\(E = \left(\right. \frac{a + a}{2} , \textrm{ } \frac{0 + a}{2} , \textrm{ } 0 \left.\right) = \left(\right. a , \textrm{ } \frac{a}{2} , \textrm{ } 0 \left.\right) .\)
3.2. (a) Chứng minh: \(\left(\right. S I C \left.\right) \bot \left(\right. S E D \left.\right)\)
\(\overset{\rightarrow}{S I} = I - S = \left(\right. \frac{a}{2} , \textrm{ } 0 , \textrm{ } 0 \left.\right) - \left(\right. \frac{a}{2} , \textrm{ } 0 , \textrm{ } \frac{\sqrt{3} \textrm{ } a}{2} \left.\right) = \left(\right. 0 , \textrm{ } 0 , \textrm{ } - \frac{\sqrt{3} \textrm{ } a}{2} \left.\right) .\) \(\overset{\rightarrow}{S C} = C - S = \left(\right. \textrm{ } a , \textrm{ } a , \textrm{ } 0 \textrm{ } \left.\right) - \left(\right. \frac{a}{2} , \textrm{ } 0 , \textrm{ } \frac{\sqrt{3} \textrm{ } a}{2} \left.\right) = \left(\right. \frac{a}{2} , \textrm{ } a , \textrm{ }\textrm{ } - \frac{\sqrt{3} \textrm{ } a}{2} \left.\right) .\)
\(\mathbf{n}_{\textrm{ } S I C} = \overset{\rightarrow}{S I} \times \overset{\rightarrow}{S C} .\)
Tính nhanh bằng định thức:
\(\mathbf{n}_{\textrm{ } S I C} = \mid \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 0 & 0 & - \textrm{ } \frac{\sqrt{3} \textrm{ } a}{2} \\ \frac{a}{2} & a & - \textrm{ } \frac{\sqrt{3} \textrm{ } a}{2} \mid = \left(\right. \textrm{ } 0 \cdot \left(\right. - \frac{\sqrt{3} a}{2} \left.\right) - \left(\right. - \frac{\sqrt{3} a}{2} \left.\right) \cdot a \left.\right) \mathbf{i} \textrm{ }\textrm{ } - \textrm{ }\textrm{ } \left(\right. \textrm{ } 0 \cdot \left(\right. - \frac{\sqrt{3} a}{2} \left.\right) - \left(\right. - \frac{\sqrt{3} a}{2} \left.\right) \cdot \frac{a}{2} \left.\right) \mathbf{j} \textrm{ }\textrm{ } + \textrm{ }\textrm{ } \left(\right. 0 \cdot a - 0 \cdot \frac{a}{2} \left.\right) \mathbf{k} .\)
Suy ra
\(\mathbf{n}_{\textrm{ } S I C} = \left(\right. \textrm{ } \underset{\frac{\sqrt{3} \textrm{ } a^{2}}{2}}{\underbrace{\textrm{ } a \cdot \frac{\sqrt{3} a}{2} \textrm{ }}} \textrm{ } , \textrm{ }\textrm{ } - \textrm{ } \underset{\textrm{ } \frac{\sqrt{3} \textrm{ } a^{2}}{4}}{\underbrace{\textrm{ } \frac{a}{2} \cdot \frac{\sqrt{3} a}{2} \textrm{ }}} \textrm{ } , \textrm{ }\textrm{ } 0 \left.\right) = \left(\right. \frac{\sqrt{3} \textrm{ } a^{2}}{2} , \textrm{ }\textrm{ } - \textrm{ } \frac{\sqrt{3} \textrm{ } a^{2}}{4} , \textrm{ }\textrm{ } 0 \left.\right) .\)
(Bỏ qua hệ số \(a^{2}\), vì chỉ cần tỉ lệ để kiểm tra vuông góc.)
\(\overset{\rightarrow}{S E} = E - S = \left(\right. a , \textrm{ } \frac{a}{2} , \textrm{ } 0 \left.\right) - \left(\right. \frac{a}{2} , \textrm{ } 0 , \textrm{ } \frac{\sqrt{3} \textrm{ } a}{2} \left.\right) = \left(\right. \frac{a}{2} , \textrm{ } \frac{a}{2} , \textrm{ } - \textrm{ } \frac{\sqrt{3} \textrm{ } a}{2} \left.\right) ,\) \(\overset{\rightarrow}{S D} = D - S = \left(\right. \textrm{ } 0 , \textrm{ } a , \textrm{ } 0 \textrm{ } \left.\right) - \left(\right. \frac{a}{2} , \textrm{ } 0 , \textrm{ } \frac{\sqrt{3} \textrm{ } a}{2} \left.\right) = \left(\right. - \textrm{ } \frac{a}{2} , \textrm{ } a , \textrm{ }\textrm{ } - \frac{\sqrt{3} \textrm{ } a}{2} \left.\right) .\)
\(\mathbf{n}_{\textrm{ } S E D} = \overset{\rightarrow}{S E} \times \overset{\rightarrow}{S D} .\)
Tính nhanh:
\(\mathbf{n}_{\textrm{ } S E D} = \mid \mathbf{i} & \mathbf{j} & \mathbf{k} \\ \frac{a}{2} & \frac{a}{2} & - \textrm{ } \frac{\sqrt{3} a}{2} \\ - \textrm{ } \frac{a}{2} & a & - \textrm{ } \frac{\sqrt{3} a}{2} \mid = \left(\right. \textrm{ } \frac{a}{2} \cdot \left(\right. - \frac{\sqrt{3} a}{2} \left.\right) - \left(\right. - \frac{\sqrt{3} a}{2} \left.\right) \cdot a \left.\right) \mathbf{i} \textrm{ }\textrm{ } - \textrm{ }\textrm{ } \left(\right. \textrm{ } \frac{a}{2} \cdot \left(\right. - \frac{\sqrt{3} a}{2} \left.\right) - \left(\right. - \frac{\sqrt{3} a}{2} \left.\right) \cdot \left(\right. - \frac{a}{2} \left.\right) \left.\right) \mathbf{j} \textrm{ }\textrm{ } + \textrm{ }\textrm{ } \left(\right. \textrm{ } \frac{a}{2} \cdot a - \frac{a}{2} \cdot \left(\right. - \frac{a}{2} \left.\right) \left.\right) \mathbf{k} .\)
Suy ra từng thành phần:
Vậy
\(\boxed{\mathbf{n}_{\textrm{ } S E D} = \left(\right. \textrm{ } \frac{\sqrt{3} a^{2}}{4} , \textrm{ }\textrm{ } \frac{\sqrt{3} a^{2}}{2} , \textrm{ }\textrm{ } \frac{3 a^{2}}{4} \left.\right) .}\)
\(\frac{a}{2} \cdot \left(\right. - \frac{\sqrt{3} a}{2} \left.\right) \textrm{ }\textrm{ } - \textrm{ }\textrm{ } \left(\right. - \frac{\sqrt{3} a}{2} \left.\right) \cdot a = - \textrm{ } \frac{\sqrt{3} a^{2}}{4} \textrm{ }\textrm{ } + \textrm{ }\textrm{ } \frac{\sqrt{3} a^{2}}{2} = \frac{\sqrt{3} a^{2}}{4} .\)
\(\frac{a}{2} \cdot \left(\right. - \frac{\sqrt{3} a}{2} \left.\right) \textrm{ }\textrm{ } - \textrm{ }\textrm{ } \left(\right. - \frac{\sqrt{3} a}{2} \left.\right) \cdot \left(\right. - \frac{a}{2} \left.\right) = - \textrm{ } \frac{\sqrt{3} a^{2}}{4} \textrm{ }\textrm{ } - \textrm{ }\textrm{ } \frac{\sqrt{3} a^{2}}{4} = - \textrm{ } \frac{\sqrt{3} a^{2}}{2} \textrm{ } ,\)
nhưng có dấu âm ở trước nên
\(\text{Th} \overset{ˋ}{\text{a}} \text{nh}\&\text{nbsp};\text{ph} \overset{ˋ}{\hat{\text{a}}} \text{n}\&\text{nbsp}; j = - \left(\right. - \frac{\sqrt{3} a^{2}}{2} \left.\right) = + \textrm{ } \frac{\sqrt{3} a^{2}}{2} .\)
\(\frac{a}{2} \cdot a \textrm{ }\textrm{ } - \textrm{ }\textrm{ } \frac{a}{2} \cdot \left(\right. - \frac{a}{2} \left.\right) = \frac{a^{2}}{2} \textrm{ }\textrm{ } + \textrm{ }\textrm{ } \frac{a^{2}}{4} = \frac{3 a^{2}}{4} .\)
\(\mathbf{n}_{\textrm{ } S I C} = \left(\right. \frac{\sqrt{3} a^{2}}{2} , \textrm{ }\textrm{ } - \textrm{ } \frac{\sqrt{3} a^{2}}{4} , \textrm{ }\textrm{ } 0 \left.\right) , \mathbf{n}_{\textrm{ } S E D} = \left(\right. \frac{\sqrt{3} a^{2}}{4} , \textrm{ }\textrm{ } \frac{\sqrt{3} a^{2}}{2} , \textrm{ }\textrm{ } \frac{3 a^{2}}{4} \left.\right) .\)
\(\mathbf{n}_{\textrm{ } S I C} \cdot \mathbf{n}_{\textrm{ } S E D} = \left(\right. \frac{\sqrt{3} a^{2}}{2} \left.\right) \left(\right. \frac{\sqrt{3} a^{2}}{4} \left.\right) \textrm{ }\textrm{ } + \textrm{ }\textrm{ } \left(\right. - \frac{\sqrt{3} a^{2}}{4} \left.\right) \left(\right. \frac{\sqrt{3} a^{2}}{2} \left.\right) \textrm{ }\textrm{ } + \textrm{ }\textrm{ } 0 \cdot \left(\right. \frac{3 a^{2}}{4} \left.\right) .\)
\(\boxed{\left(\right. S I C \left.\right) \bot \left(\right. S E D \left.\right) \textrm{ } .}\)
3.3. (b) Khoảng cách từ \(I\) đến mặt phẳng \(\left(\right. S E D \left.\right)\)
Từ \(\mathbf{n}_{\textrm{ } S E D} = \left(\right. \frac{\sqrt{3} a^{2}}{4} , \textrm{ } \frac{\sqrt{3} a^{2}}{2} , \textrm{ } \frac{3 a^{2}}{4} \left.\right)\) và “nó đi qua điểm \(S = \left(\right. \frac{a}{2} , \textrm{ } 0 , \textrm{ } \frac{\sqrt{3} a}{2} \left.\right)\)”, ta xây dựng phương trình:
\(\frac{\sqrt{3} a^{2}}{4} \textrm{ } \left(\right. x - \frac{a}{2} \left.\right) \textrm{ }\textrm{ } + \textrm{ }\textrm{ } \frac{\sqrt{3} a^{2}}{2} \textrm{ } \left(\right. y - 0 \left.\right) \textrm{ }\textrm{ } + \textrm{ }\textrm{ } \frac{3 a^{2}}{4} \textrm{ } \left(\right. z - \frac{\sqrt{3} a}{2} \left.\right) = 0.\)
\(\sqrt{3} \textrm{ } \left(\right. x - \frac{a}{2} \left.\right) \textrm{ }\textrm{ } + \textrm{ }\textrm{ } 2 \sqrt{3} \textrm{ } y \textrm{ }\textrm{ } + \textrm{ }\textrm{ } 3 \textrm{ } \left(\right. z - \frac{\sqrt{3} a}{2} \left.\right) = 0.\)
Mở ngoặc:
\(\sqrt{3} \textrm{ } x - \frac{\sqrt{3} \textrm{ } a}{2} \textrm{ }\textrm{ } + \textrm{ }\textrm{ } 2 \sqrt{3} \textrm{ } y \textrm{ }\textrm{ } + \textrm{ }\textrm{ } 3 z - \frac{3 \sqrt{3} \textrm{ } a}{2} = 0 \Longrightarrow \sqrt{3} \textrm{ } x + 2 \sqrt{3} \textrm{ } y + 3 z \textrm{ }\textrm{ } - \textrm{ }\textrm{ } 2 \sqrt{3} \textrm{ } a = 0 ,\)
vì \(- \frac{\sqrt{3} a}{2} - \frac{3 \sqrt{3} a}{2} = - 2 \sqrt{3} a .\)
\(\boxed{\textrm{ } \sqrt{3} \textrm{ } x \textrm{ }\textrm{ } + \textrm{ }\textrm{ } 2 \sqrt{3} \textrm{ } y \textrm{ }\textrm{ } + \textrm{ }\textrm{ } 3 \textrm{ } z \textrm{ }\textrm{ } - \textrm{ }\textrm{ } 2 \sqrt{3} \textrm{ } a \textrm{ }\textrm{ } = \textrm{ }\textrm{ } 0. \textrm{ }}\)
\(\mid \sqrt{3} \textrm{ } \frac{a}{2} \textrm{ }\textrm{ } + \textrm{ }\textrm{ } 2 \sqrt{3} \cdot 0 \textrm{ }\textrm{ } + \textrm{ }\textrm{ } 3 \cdot 0 \textrm{ }\textrm{ } - \textrm{ }\textrm{ } 2 \sqrt{3} \textrm{ } a \mid = \mid \textrm{ } \frac{\sqrt{3} \textrm{ } a}{2} - 2 \sqrt{3} \textrm{ } a \mid = \mid \textrm{ } - \textrm{ } \frac{3 \sqrt{3} \textrm{ } a}{2} \mid = \frac{3 \sqrt{3} \textrm{ } a}{2} .\)
\(\sqrt{\textrm{ }\textrm{ } \left(\right. \sqrt{3} \left.\right)^{2} \textrm{ }\textrm{ } + \textrm{ }\textrm{ } \left(\right. 2 \sqrt{3} \left.\right)^{2} \textrm{ }\textrm{ } + \textrm{ }\textrm{ } 3^{2} \textrm{ }\textrm{ }} = \sqrt{\textrm{ } 3 + 12 + 9 \textrm{ }} = \sqrt{24} = 2 \sqrt{6} .\)
\(d \left(\right. I , \textrm{ } \left(\right. S E D \left.\right) \left.\right) = \frac{\frac{3 \sqrt{3} \textrm{ } a}{2}}{\textrm{ } 2 \sqrt{6} \textrm{ }\textrm{ }} = \frac{3 \sqrt{3} \textrm{ } a}{2 \cdot 2 \sqrt{6}} = \frac{3 \sqrt{3} \textrm{ } a}{4 \sqrt{6}} = \frac{3 a \sqrt{18}}{4 \cdot 6} = \frac{9 a \sqrt{2}}{24} = \frac{3 a \sqrt{2}}{8} .\)
Kết quả (b):
\(\boxed{d \left(\right. I , \textrm{ } \left(\right. S E D \left.\right) \left.\right) \textrm{ }\textrm{ } = \textrm{ }\textrm{ } \frac{3 a \sqrt{2}}{8} .}\)
3.4. (c) Khoảng cách từ \(C\) đến mặt phẳng \(\left(\right. S E D \left.\right)\)
\(\sqrt{3} \textrm{ } x + 2 \sqrt{3} \textrm{ } y + 3 z - 2 \sqrt{3} a = 0\):
\(\sqrt{3} \cdot a \textrm{ }\textrm{ } + \textrm{ }\textrm{ } 2 \sqrt{3} \cdot a \textrm{ }\textrm{ } + \textrm{ }\textrm{ } 3 \cdot 0 \textrm{ }\textrm{ } - \textrm{ }\textrm{ } 2 \sqrt{3} a = \left(\right. \sqrt{3} a + 2 \sqrt{3} a - 2 \sqrt{3} a \left.\right) = \sqrt{3} \textrm{ } a .\)
Giá trị tuyệt đối: \(\mid \sqrt{3} \textrm{ } a \mid = a \sqrt{3} .\)
\(d \left(\right. C , \textrm{ } \left(\right. S E D \left.\right) \left.\right) = \frac{\textrm{ } a \sqrt{3} \textrm{ }}{\textrm{ } 2 \sqrt{6} \textrm{ }} = \frac{a \sqrt{3}}{2 \sqrt{6}} = \frac{a \sqrt{18}}{2 \cdot 6} = \frac{3 a \sqrt{2}}{12} = \frac{a \sqrt{2}}{4} .\)
Kết quả (c):
\(\boxed{d \left(\right. C , \textrm{ } \left(\right. S E D \left.\right) \left.\right) \textrm{ }\textrm{ } = \textrm{ }\textrm{ } \frac{a \sqrt{2}}{4} .}\)
3.5. (d) Khoảng cách từ \(A\) đến mặt phẳng \(\left(\right. S E D \left.\right)\)
\(\sqrt{3} \cdot 0 \textrm{ }\textrm{ } + \textrm{ }\textrm{ } 2 \sqrt{3} \cdot 0 \textrm{ }\textrm{ } + \textrm{ }\textrm{ } 3 \cdot 0 \textrm{ }\textrm{ } - \textrm{ }\textrm{ } 2 \sqrt{3} \textrm{ } a = - \textrm{ } 2 \sqrt{3} \textrm{ } a .\)
Giá trị tuyệt đối: \(2 a \sqrt{3} .\)
\(d \left(\right. A , \textrm{ } \left(\right. S E D \left.\right) \left.\right) = \frac{\textrm{ } 2 \sqrt{3} \textrm{ } a \textrm{ }}{\textrm{ } 2 \sqrt{6} \textrm{ }} = \frac{2 a \sqrt{3}}{2 \sqrt{6}} = \frac{a \sqrt{3}}{\sqrt{6}} = a \textrm{ } \sqrt{\frac{3}{6}} = a \textrm{ } \sqrt{\frac{1}{2}} = \frac{a \sqrt{2}}{2} .\)
Kết quả (d):
\(\boxed{d \left(\right. A , \textrm{ } \left(\right. S E D \left.\right) \left.\right) \textrm{ }\textrm{ } = \textrm{ }\textrm{ } \frac{a \sqrt{2}}{2} .}\)
Tóm tắt Câu 33:
a) \(\left(\right. S I C \left.\right) \bot \left(\right. S E D \left.\right)\).
b) \(d \left(\right. I , \textrm{ } \left(\right. S E D \left.\right) \left.\right) = \frac{3 a \sqrt{2}}{8} .\)
c) \(d \left(\right. C , \textrm{ } \left(\right. S E D \left.\right) \left.\right) = \frac{a \sqrt{2}}{4} .\)
d) \(d \left(\right. A , \textrm{ } \left(\right. S E D \left.\right) \left.\right) = \frac{a \sqrt{2}}{2} .\)