Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

theo định luật II niu tơn trên mặt phẳng nghiêng AB
\(\overrightarrow{F_{ms}}+\overrightarrow{N}+\overrightarrow{P}=m.\overrightarrow{a}\) (1)
chiếu (1) lên trục Ox phương song song với mặt phẳng nằm nghiêng chiều dương cùng chiều chuyển động
\(sin\alpha.P-\mu.N=m.a\) (2)
chiếu (1) lên trục Oy phương vuông gốc với mặt phẳng, chiều dương hướng lên trên
N=\(cos\alpha.P\) (3)
từ (2),(3)
\(\Rightarrow sin\alpha.g-\mu.g.cos\alpha=a\)
\(\Rightarrow a\approx4,1\)m/s2
vận tốc lúc vật tại B
\(v^2-v_0^2=2as_{AB}\Rightarrow v\approx2,875\)m/s

Vận tốc \(v=36km/h=10m/s\)
Áp dụng công thức: \(v^2-v_0^2=2aS\)
\(\Rightarrow 10^2-0^2=2.a.25\)
\(\Rightarrow a=2m/s^2\)
Lực tác dụng lên vật: \(\vec{P},\vec{N},\vec{F_k},\vec{F_{ms}}\)
Áp dụng định luật 2 Niu tơn: ta được: \(m.a=F_k-F_{ms}\Rightarrow 5.2=F_k-0,1.5.10\)
\(\Rightarrow F_k=15N\)

a) (2 điểm)
+ Vẽ hình, biểu diễn tất cả mọi lực tác dụng lên vật: (0,5 điểm)
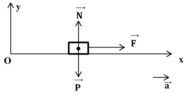
+ Viết phương trình định luật II Niu-tơn: 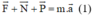 (0,5 điểm)
(0,5 điểm)
+ Chiếu pt (1) lên trục Ox ta được: F = m.a (0,5 điểm)
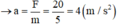 (0,5 điểm)
(0,5 điểm)
b) (2 điểm)
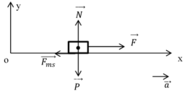
+ Vẽ hình, biểu diễn tất cả mọi lực tác dụng lên vật
+ Viết phương trình định luật II Niu-tơn
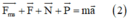 (0,5 điểm)
(0,5 điểm)
+ Chiếu pt (2) lên trục Oy: N – P = 0
→ N = P = m.g = 5.10 = 50N (0,5 điểm)
+ Độ lớn lực ma sát: F m s = μ.N = 0,2.50 = 10N (0,5 điểm)
+ Chiếu pt (2) lên trục Ox: F – F m s = ma
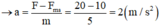 (0,5 điểm)
(0,5 điểm)

Bạn tự vẽ hình và phân tích lực nhé.
Vật chịu tác dụng của 4 lực : Fms, N , P , F (các đại lượng đều có dấu vectơ )
Theo ĐL II Niu - tơn : Fms + N + P + F = ma (các đại lượng đều có dấu vectơ kể cả a ) (1)
+Chiếu (1) lên Oy có: N - P = 0 => N= P = mg
+Chiếu (1) lên 0x có
F - Fms = ma => F - k.N = ma => F - k.m.g= ma
a)Thay số 200 - 0.25 . 40 . 10 = 40 .a => a= 2.5 ( m/s2).
b)Vận tốc của vật cuối giây thứ 3:
v= at = 2.5 . 3 = 7.5 ( m/s )
c)Đoạn đường ................:
S= at^2/2= (2.5 . 3^2)/2 = 11.25 (m)

Đáp án B.
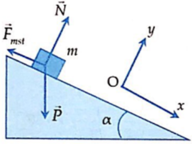
Các lực tác dụng lên vật như hình vẽ.
Áp dụng định luật II Niu-tơn:
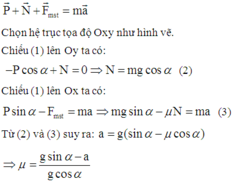

Công của hai lực \(\overrightarrow{P}\) và phản lực \(\overrightarrow{N}\) không cần quan tâm, vì vật trượt ngang nên phương di chuyển vuông góc phương 2 lực kia, công thực hiện luôn bằng không \(A_N=A_P=0\)
\(F_{ms}=\mu mg=0,2.40=8\left(N\right)\)
Coi chiều dương cùng chiều chuyển động của vật
\(A_F=F.s=20.5=100\left(J\right)\)
\(A_{Fms}=-8.5=-40\left(J\right)\)
Câu trả lời đúng là A. Fmst = μmg. Biểu thức này xác định lực ma sát trượt là tích của hệ số ma sát trượt μ, khối lượng vật m và gia tốc trọng trường g.