Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

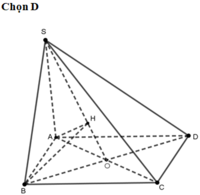
a: AC vuông góc BD
AC vuông góc SO
=>AC vuông góc (SBD)
=>SB vuông góc AC
mà AC vuông góc BD
nên AC vuông góc (SBD)
BD vuông góc AC
BD vuông góc SO
=>BD vuông góc (SAC)
=>BD vuông góc SA
b: Xét ΔACB có CO/CA=CI/CB
nên OI//AB
=>OI vuông góc BC
BC vuông góc OI
BC vuông góc SO
=>BC vuông góc (SOI)
=>(SBC) vuông góc (SOI)

Bạn vẽ hình giúp mình nha ^^
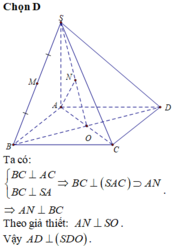
Xét (ABCD), kẻ \(MH\perp AB\left(H\in AB\right)\)
Xét (SAB), kẻ HF//SB(\(F\in SA\))
Có: \(\left\{{}\begin{matrix}MH\perp AB\\MH\perp SA\end{matrix}\right.\)\(\Rightarrow MH\perp\left(SAB\right)\)\(\Rightarrow MH\perp HF\)
Ta có: \(\alpha=\left(\stackrel\frown{SB,AM}\right)=\left(\stackrel\frown{HF,MH}\right)=arccos\left(\dfrac{HA}{HF}\right)\)
Xét \(\Delta AHF\) vuông tại A có: \(HF^2=HA^2+AF^2=a^2+\left(\dfrac{a}{2}\right)^2=\dfrac{5}{4}a^2\Rightarrow HF=\dfrac{a\sqrt{5}}{2}\)
\(\Rightarrow\alpha=arccos\left(\dfrac{HA}{HF}\right)=arccos\left(\dfrac{2a}{a\sqrt{5}}\right)\approx26,57^o\) \(\Rightarrow cos\alpha=\dfrac{HA}{HF}=\dfrac{2a}{a\sqrt{5}}=\dfrac{2}{\sqrt{5}}\)
là \(cos^{-1}\) trong máy tính á, đại loại kiểu ngược lại của cos... sin/cos/tan/sin sẽ đi với góc, còn arc + sin/cos/tan/cot là các cạnh ứng với công thức sin/cos/tan/cot

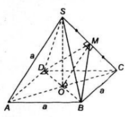
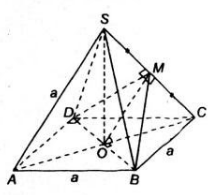
a) Theo giả thiết, S.ABCD là hình chóp đều và đáy ABCD là hình vuông nên SO ⊥ (ABCD) ( tính chất hình chóp đều)
Đáy ABCD là hình vuông cạnh a nên
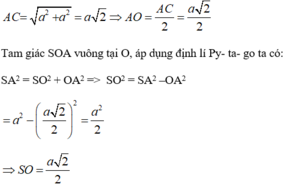

=> Góc giữa hai mặt phẳng (MBD) và (ABCD) là 45 o