Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

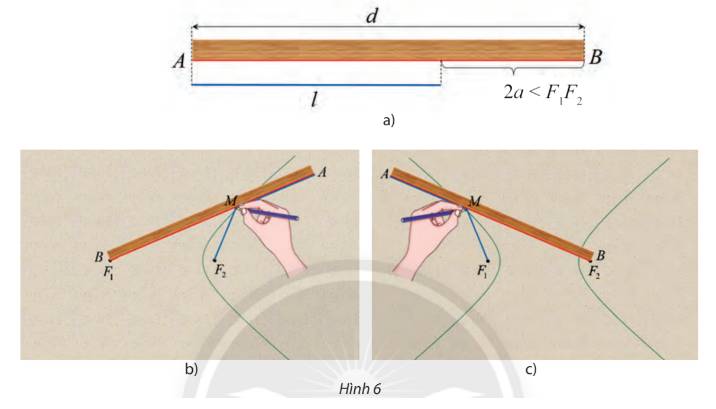
Khi M thay đổi, hiệu \(M{F_1} - M{F_2} = \left( {M{F_1} + MA} \right) - \left( {M{F_2} + MA} \right) = AB - l{\rm{ }}\)không đổi.

a) Đường vừa nhận được là đường “màu đỏ” trong Hình 7.17.
b) Tổng khoảng cách từ đẩu bút đến các vị trí không thay đổi.

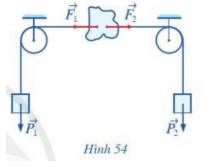
a) Trọng lực của hai vật đều hướng xuống, vuông góc với mặt đất, đo dó chúng cùng phương, cùng hướng với nhau.
Hơn nữa: Công thức tính độ lớn trọng lực là: \(P = mg\).
Hai vật có khối lượng như nhau, do đó \({P_1} = {P_2}\)
Vậy \(\overrightarrow {{P_1}} = \overrightarrow {{P_2}} \)
b) Do trọng lực tạo thành lực kéo lên mảnh nhựa nên độ lớn của các lực \(\overrightarrow {{F_1}} ,\;\overrightarrow {{F_2}} \) là như nhau.
Chúng có hướng ngược nhau.

Khi M thay đổi, ta có: \(M{F_1} + M{F_2} +{F_1}{F_2} =\) độ dài vòng dây
⇒ Tổng độ dài \(M{F_1} + M{F_2}\) là một độ dài không đổi (độ dài vòng dây - {F_1}{F_2}).

a) Khi điểm M trùng với điểm A ta có:
\(M{F_1} - M{F_2} = A{F_1} - A{F_2} = AB - A{F_2} = d - l = 2a\)
b) Tương tự khi điểm M trùng với điểm A ta có:
\(M{F_2} - M{F_1} = A{F_2} - A{F_1} = AB - A{F_1} = d - l = 2a\)

Đầu tiên, cứ gọi 2 sợi dây là A và B cho dễ nhé. Muốn giải được câu đố này, bạn phải dựa vào dữ kiện duy nhất được cung cấp: A và B đều cháy hết trong vòng 1 giờ đồng hồ khi đốt cháy một đầu.
Điều này có nghĩa là nếu đốt cháy 2 đầu, sợi dây sẽ cháy trong đúng 30 phút. Và sau khi cháy được một nửa, bạn đốt nốt đầu còn lại, thì khoảng thời gian cho đoạn dây còn lại cháy hết sẽ đúng bằng 15 phút.
Vậy vấn đề bây giờ chỉ là làm cách nào đo được chính xác thời điểm đoạn dây cháy còn một nửa mà thôi.
Dễ quá rồi đúng không: Với dây A, hãy đốt cháy 2 đầu, đồng thời đốt một đầu của dây B.

Đáp án của câu đố kinh điển trên.
Khi dây A cháy hết, dây B sẽ còn 30 phút nữa để cháy. Giờ hãy châm lửa vào đầu còn lại của dây B, và khi B cháy hết, chính xác 45 phút đã trôi qua.
nha hoc24

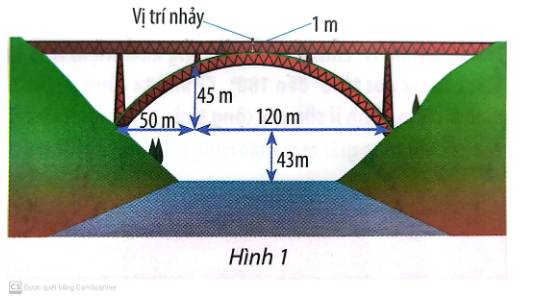
Gọi \(y = f(x) = a{x^2} + bx + c\) là công thức của hàm số có đồ thị là hình ảnh của bộ phận chống đỡ.
Chọn hệ trục tọa độ Oxy như hình dưới:
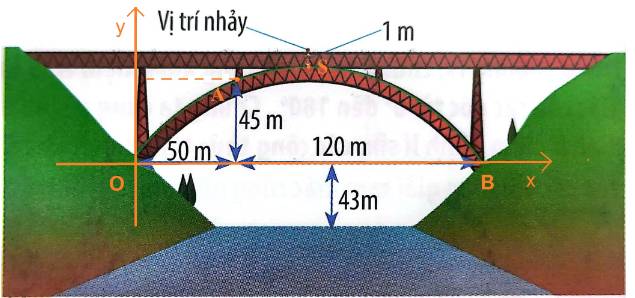
Gọi S là đỉnh của parabol, dưới vị trí nhảy 1m.
A, B là các điểm như hình vẽ.
Dễ thấy: A (50; 45) và B (120+50; 0) = (170; 0).
Các điểm O, A, B đều thuộc đồ thị hàm số.
Do đó:
\(f(0) = a{.0^2} + b.0 + c = 0 \Leftrightarrow c = 0\)
\(f(50) = a{.50^2} + b.50 + c = 45 \Leftrightarrow a{.50^2} + b.50 = 45\)
\(f(170) = a{.170^2} + b.170 + c = 0 \Leftrightarrow a{.170^2} + b.170 = 0 \Leftrightarrow a.170+ b = 0\)
Giải hệ phương trình \(\left\{ \begin{array}{l}a{.50^2} + b.50 = 45\\a.170 + b = 0\end{array} \right.\) ta được \(a = - \frac{{3}}{{400}};b = \frac{{51}}{{40}}\)
Vậy \(y = f(x) = - \frac{{3}}{{400}}{x^2} + \frac{{51}}{{40}}x\)
Đỉnh S có tọa độ là \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - \frac{{51}}{{40}}}}{{2.\left( { - \frac{{3}}{{400}}} \right)}} = 85;\;{y_S} = - \frac{{3}}{{400}}.8{5^2} + \frac{{51}}{{40}}.85 = \frac{{867}}{{16}} \approx 54,2\)
Khoảng cách từ vị trí bắt đầu nhảy đến mặt nước là: \(1 + 54,2 + 43 = 98,2(m)\)
Vậy chiều dài của sợi dây đó là: \(98,2:3 \approx 32,7\,(m)\)

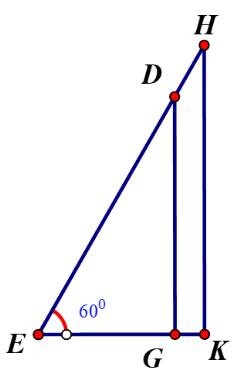
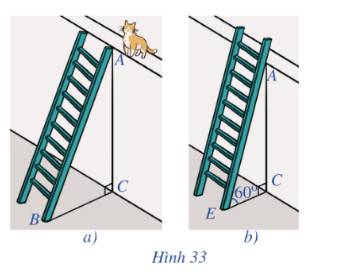
Gọi chiều cao bức tường DG là x (m) (x>0)
Chiều dài chiếc thang là x+1 (m)
Khoảng cách từ chân thang sau khi bác Nam điều chỉnh là: \(EG = \frac{{DG}}{{\sqrt 3 }} = \frac{{x\sqrt 3 }}{3}\) (m)
Áp dụng định lý Py-ta-go cho tam giác vuông ABC ta có:
\(BC = \sqrt {{{\left( {x + 1} \right)}^2} - {x^2}} \)(m)
Bác Nam dịch chuyển chân thang vào gần chân tường thêm 0,5 m nên ta có:
\(\sqrt {{{\left( {x + 1} \right)}^2} - {x^2}} - 0,5 = \frac{{x\sqrt 3 }}{3}\)
\(\begin{array}{l} \Leftrightarrow \sqrt {{{\left( {x + 1} \right)}^2} - {x^2}} = \frac{x}{{\sqrt 3 }} + 0,5\\ \Leftrightarrow \sqrt {2x + 1} = \frac{x}{{\sqrt 3 }} + 0,5\left( * \right)\end{array}\)
Ta có \(\frac{x}{{\sqrt 3 }} + 0,5 \ge 0 \Leftrightarrow \frac{x}{{\sqrt 3 }} \ge - \frac{1}{2}\)\( \Leftrightarrow x \ge - \frac{{\sqrt 3 }}{2}\) (Luôn đúng do x>0)
Ta bình phương hai vế (*) ta được:
\(\begin{array}{l}2x + 1 = {\left( {\frac{x}{{\sqrt 3 }} + 0,5} \right)^2}\\ \Leftrightarrow 2x + 1 = \frac{{{x^2}}}{3} + \frac{x}{{\sqrt 3 }} + 0,25\\ \Leftrightarrow \frac{{{x^2}}}{3} + \left( {\frac{{\sqrt 3 }}{3} - 2} \right)x - \frac{3}{4} = 0\\ \Leftrightarrow \left[ \begin{array}{l}x \approx 4,7\left( {tm} \right)\\x \approx - 0,5\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy chiều cao của bức tường là 4,7 m.