K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
3 tháng 1 2024
Câu 2:
a: Để (d1) cắt (d2) thì \(m-1\ne3-m\)
=>\(2m\ne4\)
=>\(m\ne2\)
b: Thay m=0 vào (d1), ta được:
\(y=\left(0-1\right)x+2=-x+2\)
Thay m=0 vào (d2), ta được:
\(y=\left(3-0\right)x-2=3x-2\)
Vẽ đồ thị:
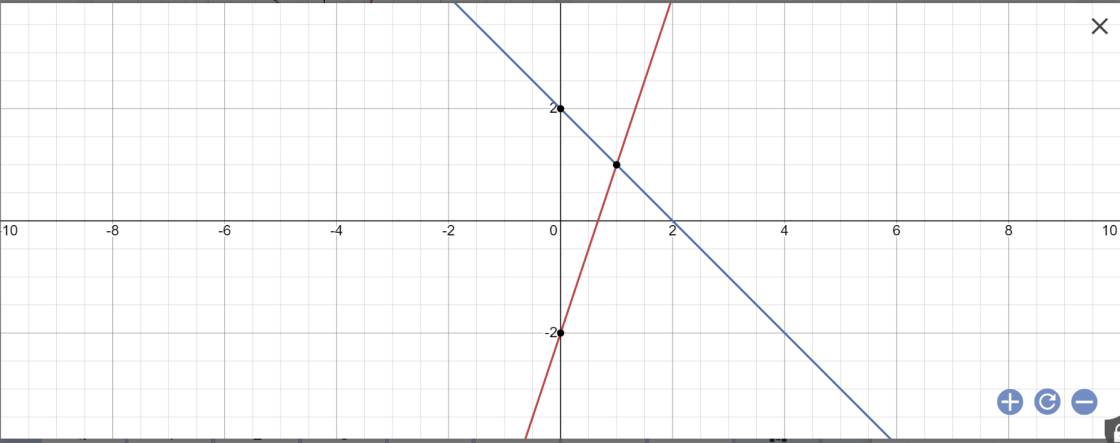
c: Phương trình hoành độ giao điểm là:
3x-2=-x+2
=>3x+x=2+2
=>4x=4
=>x=1
Thay x=1 vào y=3x-2, ta được:
y=3*1-2=3-2=1
d:
Khi m=0 thì (d2): y=3x-2
Gọi \(\alpha\) là góc tạo bởi (d2): y=3x-2 với trục Ox
y=3x-2 nên a=3
\(tan\alpha=a=3\)
=>\(\alpha\simeq72^0\)
Câu 3:
a: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OM là đường trung trực của AB
=>OM\(\perp\)AB tại H và H là trung điểm của AB
Xét ΔOAM vuông tại A có AH là đường cao
nên \(OH\cdot OM=OA^2\)
=>\(OH\cdot OM=R^2\)
b: Ta có: AC//OM
OM\(\perp\)AB
Do đó: AB\(\perp\)AC
=>ΔABC vuông tại A
=>ΔABC nội tiếp đường tròn đường kính BC
mà ΔABC nội tiếp (O)
nên O là trung điểm của BC
=>B,O,C thẳng hàng
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
=>BE\(\perp\)EC tại E
=>BE\(\perp\)CM tại E
Xét ΔMBC vuông tại B có BE là đường cao
nên \(ME\cdot MC=MB^2\)(3)
Xét ΔMBO vuông tại B có BH là đường cao
nên \(MH\cdot MO=MB^2\left(4\right)\)
Từ (3) và (4) suy ra \(ME\cdot MC=MH\cdot MO\)
DD
Đoàn Đức Hà
Giáo viên
9 tháng 6 2021
Gọi số câu trả lời đúng ở mỗi phần lần lượt là \(a,b\)câu, \(a,b\inℕ^∗;a\le8;b\le10\).
Số câu trả lời sai ở phần A là \(10-2-a=8-a\)(câu).
Tổng số điểm Nam đạt được là:
\(4a-\left(8-a\right)+6b=49\)
\(\Leftrightarrow5a+6b=57\)
Ta có: \(6\equiv1\left(mod5\right)\Rightarrow6b\equiv b\left(mod5\right)\)mà \(57\equiv2\left(mod5\right)\)nên \(b\equiv2\left(mod5\right)\)
do đó \(b=2\)hoặc \(b=7\).
Thử \(2\)giá trị trên chỉ thu được một nghiệm thỏa mãn là \(\left(a,b\right)=\left(3,7\right)\).
Vậy số câu trả lời đúng của Nam ở mỗi phần lần lượt là \(3,7\)câu.
Anh Vi Cá Đuối báo trc là bn ấy lm sai r nha !!
NLPT ai cho chuyển \(\sqrt{a}-1\) lên hay vậy lỡ âm sao!!
VD: \(-2>-3\Leftrightarrow\frac{2}{-1}>\frac{3}{-1}\Leftrightarrow2>3\left(vl\right)\)
báo lun là mk hơi sai ở đkxd nha !! x ≥ 0 ms đúng !!
Bài 1:
2:
a) Ta có: \(M=\left(1+\frac{\sqrt{a}}{a+1}\right):\left(\frac{1}{\sqrt{a}-1}-\frac{2\sqrt{a}}{a\sqrt{a}+\sqrt{a}-a-1}\right)\)
\(=\left(\frac{a+1+\sqrt{a}}{a+1}\right):\left(\frac{a+1}{\left(a+1\right)\left(\sqrt{a}-1\right)}-\frac{2\sqrt{a}}{\left(a+1\right)\left(\sqrt{a}-1\right)}\right)\)
\(=\frac{a+1+\sqrt{a}}{a+1}:\frac{\left(\sqrt{a}-1\right)^2}{\left(\sqrt{a}-1\right)\left(a+1\right)}\)
\(=\frac{a+\sqrt{a}+1}{a+1}:\frac{\sqrt{a}-1}{a+1}\)
\(=\frac{a+\sqrt{a}+1}{\sqrt{a}-1}\)
b) Để M>1 thì \(\frac{a+\sqrt{a}+1}{\sqrt{a}-1}>1\)
\(\Leftrightarrow a+\sqrt{a}+1>\sqrt{a}-1\)
\(\Leftrightarrow a+\sqrt{a}+1-\sqrt{a}+1>0\)
\(\Leftrightarrow a+2>0\)
\(\Leftrightarrow a>-2\)
mà \(a\ge0\left(đkxđ\right)\)
nên \(a\ge0\)
Vậy: Khi a không âm và a\(\ne\)1 thì M>1