Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có m = 300 tấn = 3.105 kg; F = 440 kN = 4,4.105 N; v = 285 km/h = 475/6 m/s
Gia tốc của máy bay là: \(a = \frac{F}{m} = \frac{{4,{{4.10}^5}}}{{{{3.10}^5}}} = \frac{{22}}{{15}}(m/{s^2})\)
Chiều dài tối thiểu của đường băng để đảm bảo máy bay cất cánh được là:
\(s = \frac{{{v^2} - v_0^2}}{{2.a}} = \frac{{{{\left( {\frac{{475}}{6}} \right)}^2}}}{{2.\frac{{22}}{{15}}}} \approx 2136,6(m)\)

Áp dụng định luật II Niu-tơn cho chuyển động của máy bay :
F - F m s = ma ⇒ F - μ P = (P/g).( v 2 /2s)
với F là lực kéo của động cơ, F m s là lực ma sát với đường băng, a là gia tốc của máy bay khối lượng m trên đoạn đường băng dài s. Từ đó suy ra :
![]()
Như vậy, động cơ máy bay phải có công suất tối thiểu bằng:
P = Fv = 5,2. 10 3 .25. ≈ 130 kW

Đổi 297 km/h = 82,5 m/s
Gia tốc trung bình của máy bay trong quá trình bay là:
\(a = \frac{{{v_2} - {v_1}}}{{{t_2} - {t_1}}} = \frac{{82,5}}{{30}} = 2,75(m/{s^2})\)

Gia tốc vật:
\(a=\dfrac{F_k}{m}=\dfrac{4}{2}=2\)m/s2
Sau khi đi được 9m kể từ lúc bắt đầu \(\left(v_0=0\right)\) thì vật đạt vận tốc: \(v^2-v^2_0=2aS\)
\(\Rightarrow v=\sqrt{2aS}=\sqrt{2\cdot2\cdot9}=6\)m/s

Gia tốc vật:
\(a=\dfrac{F_k}{m}=\dfrac{4}{2}=2\)m/s2
Sau khi đi được 9m thì vật đạt vận tốc:
\(v^2-v^2_0=2aS\)
\(\Rightarrow v=\sqrt{2aS+v^2_0}=\sqrt{2\cdot2\cdot9+0^2}=6\)m/s

a) Đổi 198km/h = 55m/s
Gia tốc của máy bay:
Ta có: \(v^2-v^2_0=2as\Leftrightarrow a=\dfrac{v^2-v^2_0}{2s}=\dfrac{55^2-0^2}{2.100}=15,125\left(m/s^2\right)\)
b) Thời gian máy bay tăng tốc:
Ta có: \(v=v_0+at\Leftrightarrow t=\dfrac{v-v_0}{a}=\dfrac{55-0}{15,125}=\dfrac{40}{11}\left(s\right)=3,6363\left(s\right)\)

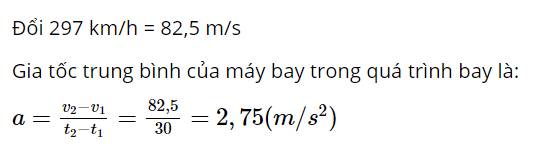
Vật bắt đầu cất cánh có \(v_0=0\).
\(v=250km/h=\dfrac{625}{9}m/s\)
Gia tốc vật: \(a=\dfrac{v^2-v_0^2}{2S}=\dfrac{\left(\dfrac{625}{9}\right)^2-0}{2\cdot4000}=0,6m/s^2\)
Lực phát động của máy bay:
\(F=m\cdot a=500\cdot1000\cdot0,6=3\cdot10^5N\)