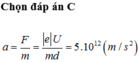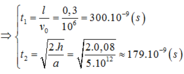Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

N q1 q2 A E1 E2
Ta có:
\(E_1=\dfrac{9.10^9.4.10^{-8}}{\left(\dfrac{5}{100}\right)^2}=144000\left(v/m\right)\)
\(E_2=\dfrac{9.10^9.4.10^{-8}}{\left(\dfrac{15}{100}\right)^2}=16000\left(v/m\right)\)
\(\Rightarrow E=\left|E_1-E_2\right|=128000\left(v/m\right)\)

Gọi H là trung điểm của AB và M là điểm nằm trên đường trung trực của AB.
Độ lớn hai điện tích bằng nhau và M cách đều hai điện tích.
Do \(E_1=E_2\) nên \(E=2E_1\cdot cos\alpha=2\cdot k\cdot q\cdot\dfrac{x}{\sqrt{\left(x^2+a^2\right)^2}}\)
\(E_{M_{max}}\Leftrightarrow\sqrt{\left(x^2+a^2\right)^2}_{min}\)
\(\Leftrightarrow x=a\)

Vận tốc cực đại của electron bắn ra từ catode là \(v\). Ta có:
\(\frac{mv^2}{2}=eU_h\) (\(U_h=2V\) là hiệu điện thế hãm)
\(\Rightarrow v=\sqrt{\frac{2U_he}{m}}=8,4.10^5\text{(m/s)}\)
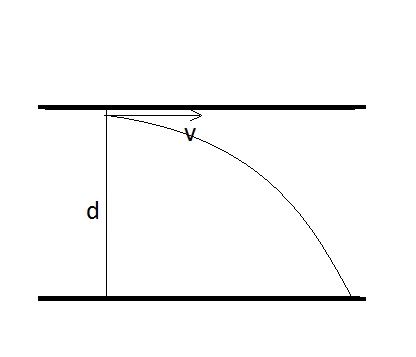
Vận tốc này có thế theo mọi hướng, để đập vào anode với bán kính lớn nhất thì electron sẽ có vận tốc theo phương song song với bản phẳng.
|
\(t=\sqrt{\frac{2d}{a}}=\sqrt{\frac{2d^2m_e}{U_e}}=2,4.10^{-8}\left(s\right)\)
Bán kính lớn nhất:
\(r=vt=0,02\left(m\right)=2\left(cm\right)\)
\(chọn.A\)