Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(x^3-\dfrac{1}{9}x=0\)
\(\Rightarrow x\left(x^2-\dfrac{1}{9}\right)=0\)
\(\Rightarrow x\left(x-\dfrac{1}{3}\right)\left(x+\dfrac{1}{3}\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x-\dfrac{1}{3}=0\Leftrightarrow x=\dfrac{1}{3}\\x+\dfrac{1}{3}=0\Leftrightarrow x=-\dfrac{1}{3}\end{matrix}\right.\)
b) \(x\left(x-3\right)+x-3=0\)
\(\Rightarrow\left(x-3\right)\left(x+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-3=0\Rightarrow x=3\\x+1=0\Rightarrow x=-1\end{matrix}\right.\)
c) \(2x-2y-x^2+2xy-y^2=0\) (thêm đề)
\(\Rightarrow2\left(x-y\right)-\left(x-y\right)^2=0\)
\(\Rightarrow\left(x-y\right)\left(2-x+y\right)=0\)
\(\Rightarrow\left\{{}\begin{matrix}x-y=0\Rightarrow x=y\\2-x+y=0\Rightarrow x-y=2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=y\left(1\right)\\\left(1\right)\Rightarrow x-x=2\left(loại\right)\end{matrix}\right.\)
d) \(x^2\left(x-3\right)+27-9x=0\)
\(\Rightarrow x^2\left(x-3\right)+\left(x-3\right).9=0\)
\(\Rightarrow\left(x-3\right)\left(x^2+9\right)=0\)
\(\Rightarrow x-3=0\Rightarrow x=3.\)


a
Dễ thấy \(\Delta\)BEC và \(\Delta\)DCF đồng dạng ( g.g ) nên \(\frac{BE}{DC}=\frac{EC}{CF}=\frac{BC}{DF}\)
\(\Rightarrow\)BE.DF=BC.DC=BC2 không đổi
b
Ta có:^ABD=\(\frac{1}{2}\)^ABC=\(\frac{1}{2}\)1200=600 \(\Rightarrow\)^EBD=1800-600=1200
Tương tự:^BDF=1200
Ta có:\(\frac{EB}{BC}=\frac{CD}{DF}\Rightarrow\frac{BE}{BD}=\frac{BD}{DF}\) ( để ý góc A bằng 600 và ABCD là hình thoy )
Khi đó \(\Delta\)EBD và \(\Delta\)BDF đồng dạng ( c.g.c ) \(\Rightarrow\)^DBF=^BED
Mà ^BED+^BDI=1200 nên ^DBI+^BDI=1200 hay ^BID=1200
c
Để nghĩ sau
Cảm ơn bạn nhiều nha, bạn giỏi quá. Đây là lần thứ 2 mình đăng câu hỏi, mình cần rất gấp mà lần đầu không ai giúp mình :(((
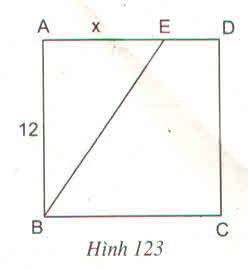
 AB.AE =
AB.AE =  hay 6x =
hay 6x = 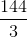
Bài 1
A B C H D \(S_{ABCD}=AH.AB=AH.AD=18\Leftrightarrow AD=6\) Tam giác AHD vuông tại H có \(\frac{AD}{AH}=\frac{6}{3}=2\) \(\Leftrightarrow\widehat{D}=30_{^{ }}\)\(\Leftrightarrow\widehat{A}=150\) Bài 2 A B C D E H Vẽ \(EH\perp AD\).Ta có ABCD là hình chữ nhật nên \(EH=AB\) \(\Rightarrow S_{ADE}=\frac{EH.AD}{2}=\frac{AB.AD}{2}=50\) Bài 3 Mình cho \(\widehat{D}=60\) A B C D O Ta có: ADC là tam giác đều nên \(S_{ADC}=\frac{\sqrt{3}}{4}AD^2\)(cái này bạn dùng Pythagos chứng minh giùm mình nha) Tương tự:\(S_{ABC}=\frac{\sqrt{3}}{4}AB^2=\frac{\sqrt{3}}{4}AD^2\) \(S_{ABC}+S_{ADC}=S_{ABCD}=2.\frac{\sqrt{3}}{4}AD^2=\frac{\sqrt{3}}{2}AD^2=8\sqrt{3}\) \(\Leftrightarrow AD^2=8\sqrt{3}.\frac{2}{\sqrt{3}}16\)\(\Leftrightarrow AD=4\) \(\Leftrightarrow AB+BC+CD+DA=4AD=16\) Chu vi tam giác ABCD là 16
bạn tự vẽ hình nhé mình đang lười: Tam giác đều ABC đường cao AH: Xét tam giác AHB vuông tại H có:\(AH^2+HB^2=AB^2\) lại có:\(\widehat{HAB}=30\Leftrightarrow HB=\frac{1}{2}AB\) tức là :\(AH^2+\left(\frac{1}{2}AB\right)^2=AB^2\Leftrightarrow AH^2=\frac{3}{4}AB^2\Leftrightarrow AH=\frac{\sqrt{3}}{2}AB\)\(S_{ABC}=\frac{AH.BC}{2}=\frac{AB.\frac{\sqrt{3}}{2}AB}{2}=\frac{\sqrt{3}}{4}AB^2\)