Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔMND vuông tại M và ΔHND vuông tại H có
ND chung
\(\widehat{MND}=\widehat{HND}\)(ND là tia phân giác của \(\widehat{MNH}\))
Do đó: ΔMND=ΔHND(cạnh huyền-góc nhọn)


nếu bạn ko thấy ảnh thì zô thống kê hỏi đáp của mình là thấy bài này nhá . ( cậu tìm câu nào có câu này r ấn zô xem nha )
hoặc link bài của mình nè
https://scontent-hkt1-1.xx.fbcdn.net/v/t1.15752-9/89947717_345887062999332_7304147707155709952_n.jpg?_nc_cat=110&_nc_sid=b96e70&_nc_ohc=Hj57duZ44dcAX91P2ra&_nc_ht=scontent-hkt1-1.xx&oh=7ea184f17776bd230198145c38f92aae&oe=5E95F1D5

M P N 3 4 A C G
a) xét \(\Delta MNP\)VUÔNG TẠI M CÓ
\(\Rightarrow NP^2=MN^2+MP^2\left(PYTAGO\right)\)
THAY\(NP^2=4^2+3^2\)
\(NP^2=16+9\)
\(NP^2=25\)
\(\Rightarrow NP=\sqrt{25}=5\left(cm\right)\)
XÉT \(\Delta MNP\)CÓ
\(\Rightarrow NP>MN>MP\left(5>4>3\right)\)
\(\Rightarrow\widehat{M}>\widehat{P}>\widehat{N}\)( QUAN HỆ GIỮA CẠNH VÀ GÓC ĐỐI DIỆN)
B) xét \(\Delta\text{ CPM}\)VÀ\(\Delta\text{CPA}\)CÓ
\(PM=PA\left(GT\right)\)
\(\widehat{MPC}=\widehat{APC}=90^o\)
PC LÀ CAH CHUNG
=>\(\Delta\text{ CPM}\)=\(\Delta\text{CPA}\)(C-G-C)
c)
\(\Delta CPM=\Delta CPA\left(cmt\right)\)
\(\Rightarrow\widehat{CMP}=\widehat{CPA}\left(\text{hai góc tương ứng}\right)\)
\(\text{Ta có: }\)\(\widehat{MNA}+\widehat{NAM}=90^o\left(\Delta MNA\perp\text{ tại M}\right)\)
\(\widehat{NMC}+\widehat{CMP}=90^o\)
\(\Rightarrow\widehat{MNA}+\widehat{NAM}=\)\(\widehat{NMC}+\widehat{CMP}\)
\(\Rightarrow\widehat{MNA}=\widehat{NMC}\left(\widehat{CMP}=\widehat{NAM}\right)\)
\(Hay:\)\(\widehat{MNC}=\widehat{NMC}\)
\(\Rightarrow\Delta NMC\text{ cân}\)
\(\Rightarrow CN=CM\left(đpcm\right)\)

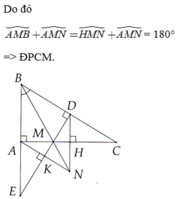
a) Do ND là đường phân giác của ∆MNP (gt)
⇒ ∠MND = ∠PND
⇒ ∠MND = ∠HND
Xét hai tam giác vuông: ∆MND và ∆HND có:
ND là cạnh chung
∠MND = ∠HND (cmt)
⇒ ∆MND = ∆HND (cạnh huyền - góc nhọn)
b) Do ∆MND = ∆HND (cmt)
⇒ MN = HN (hai cạnh tương ứng)
c) Do ∆MND = ∆HND (cmt)
⇒ MD = HD (hai cạnh tương ứng)
Xét hai tam giác vuông: ∆DMK và ∆DHP có:
MD = HD (cmt)
∠MDK = ∠HDP (đối đỉnh)
⇒ ∆DMK = ∆DHP (cạnh góc vuông - góc nhọn kề)
⇒ MK = HP (hai cạnh tương ứng)
Lại có: MN = HN (cmt)
⇒ MK + MN = HP + HN
⇒ KN = PN
⇒ ∆NPK cân tại N
Do ∆MNP vuông tại M (gt)
⇒ PM ⊥ MN
⇒ PM ⊥ NK
⇒ PM là đường cao của ∆NPK
Lại có:
DH ⊥ NP (gt)
⇒ KH ⊥ NP
⇒ KH là đường cao thứ hai của ∆NPK
⇒ ND là đường cao thứ ba của ∆NPK
Mà ∆NPK cân tại N (cmt)
⇒ ND cũng là đường trung tuyến của ∆NPK
⇒ ND đi qua trung điểm của PK
Mà I là trung điểm của PK
⇒ N, D, I thẳng hàng