Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trên bờ bên kia của dòng sông lấy điểm B, bờ bên này lấy điểm A đối diện với B. Để đo gián tiếp độ rộng của dòng sông (khoảng cách AB), người ta lấy điểm C bên này sông và cách A một khoảng AC = 80 mét, đặt giác kế tại C và đo được góc ^ACB = 34o. Tính chiều rộng AB của con sông?
( Cho biết: sin34o = 0,56 ; cos34o = 0,83 ; tg34o = 0,67 ; cotg34o = 1,48 )

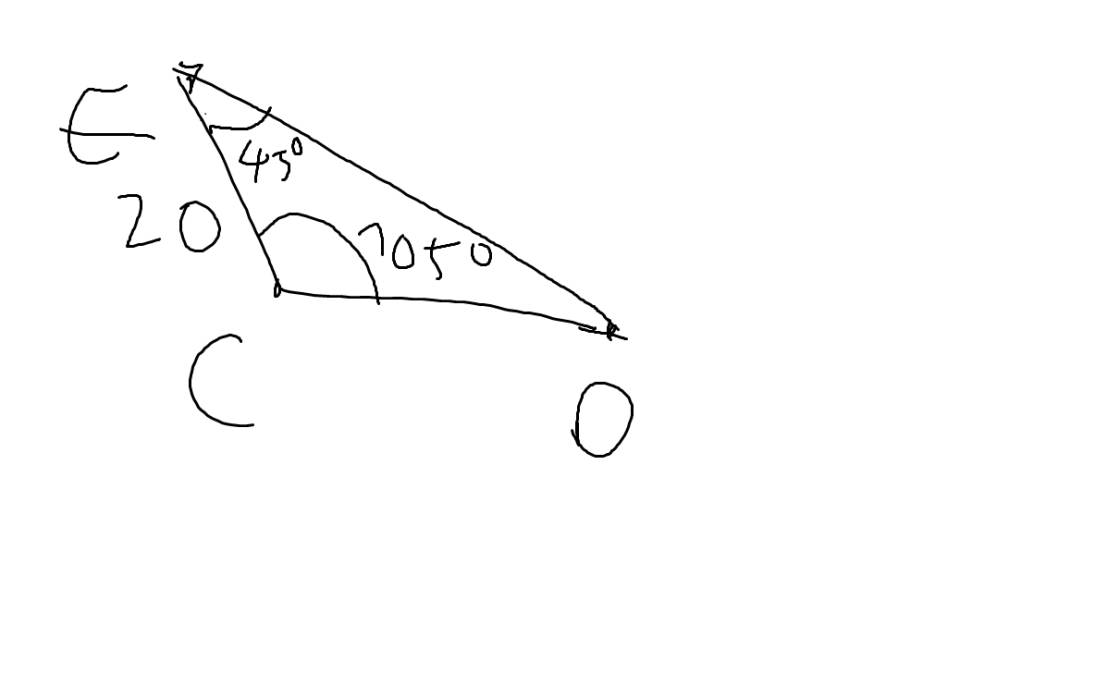
Xét ΔCED có \(\widehat{C}+\widehat{D}+\widehat{E}=180^0\)
=>\(\widehat{D}+105^0+45^0=180^0\)
=>\(\widehat{D}=30^0\)
Xét ΔCED có \(\dfrac{CE}{sinD}=\dfrac{CD}{sinE}\)
=>\(\dfrac{CD}{sin45}=\dfrac{20}{sin30}\)
=>\(\dfrac{CD}{sin45}=\dfrac{20}{\dfrac{1}{2}}=40\)
=>\(CD=40\cdot sin45=40\cdot\dfrac{\sqrt{2}}{2}=20\sqrt{2}\)

Câu 1: Tam giác ABC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền BC
=> AM=\(\frac{1}{2}\)BC mà AM=6 cm=> BC=12cm.
Tam giác ANB vuông tại A có AN2+AB2=BN2 (Theo Pytago) mà BN=9cm (gt)
=>AN2+AB2=81 Lại có AN=\(\frac{1}{2}\)AC =>\(\frac{1}{2}\)AC2+AB2=81 (1)
Tam giác ABC vuông tại A có: AC2+AB2=BC2 => BC2 - AB2 = AC2 (2)
Từ (1) và (2) suy ra \(\frac{1}{4}\)* (BC2 - AB2)+AB2=81 mà BC=12(cmt)
=> 36 - \(\frac{1}{4}\)AB2+AB2=81
=> 36+\(\frac{3}{4}\)AB2=81
=> AB2=60=>AB=\(\sqrt{60}\)
C2
Cho hình thang cân ABCD có đáy lớn CD = 1
C4
Câu hỏi của Thiên An - Toán lớp 9 - Học toán với OnlineMath

Ta có: ΔABC đều, D ∈ AB, DE⊥AB, E ∈ BC
=> ΔBDE có các góc với số đo lần lượt là: 300
; 600
; 900
=> BD=1/2BE
Mà BD=1/3BA => BD=1/2AD => AD=BE => AB-AD=BC-BE (Do AB=BC)
=> BD=CE.
Xét ΔBDE và ΔCEF: ^BDE=^CEF=900
; BD=CE; ^DBE=^ECF=600
=> ΔBDE=ΔCEF (g.c.g) => BE=CF => BC-BE=AC-CF => CE=AF=BD
Xét ΔBDE và ΔAFD: BE=AD; ^DBE=^FAD=600
; BD=AF => ΔBDE=ΔAFD (c.g.c)
=> ^BDE=^AFD=900
=>DF⊥AC (đpcm).
b) Ta có: ΔBDE=ΔCEF=ΔAFD (cmt) => DE=EF=FD (các cạnh tương ứng)
=> Δ DEF đều (đpcm).
c) Δ DEF đều (cmt) => DE=EF=FD. Mà DF=FM=EN=DP => DF+FN=FE+EN=DE+DP <=> DM=FN=EP
Lại có: ^DEF=^DFE=^EDF=600=> ^PDM=^MFN=^NEP=1200
(Kề bù)
=> ΔPDM=ΔMFN=ΔNEP (c.g.c) => PM=MN=NP => ΔMNP là tam giác đều.
d) Gọi AH; BI; CK lần lượt là các trung tuyến của ΔABC, chúng cắt nhau tại O.
=> O là trọng tâm ΔABC (1)
Do ΔABC đều nên AH;BI;BK cũng là phân giác trong của tam giác => ^OAF=^OBD=^OCE=300
Đồng thời là tâm đường tròn ngoại tiếp tam giác => OA=OB=OC
Xét 3 tam giác: ΔOAF; ΔOBD và ΔOCE:
AF=BD=CE
^OAF=^OBD=^OCE => ΔOAF=ΔOBD=ΔOCE (c.g.c)
OA=OB=OC
=> OF=OD=OE => O là giao 3 đường trung trực Δ DEF hay O là trọng tâm Δ DEF (2)
(Do tam giác DEF đề )
/
(Do tam giác DEF đều)
Dễ dàng c/m ^OFD=^OEF=^ODE=300
=> ^OFM=^OEN=^ODP (Kề bù)
Xét 3 tam giác: ΔODP; ΔOEN; ΔOFM:
OD=OE=OF
^ODP=^OEN=^OFM => ΔODP=ΔOEN=ΔOFM (c.g.c)
OD=OE=OF (Tự c/m)
=> OP=ON=OM (Các cạnh tương ứng) => O là giao 3 đường trung trực của ΔMNP
hay O là trọng tâm ΔMNP (3)
Từ (1); (2) và (3) => ΔABC; Δ DEF và ΔMNP có chung trọng tâm (đpcm).
Câu 3:
Xét ΔBEC vuông tại E và ΔADC vuông tại D có
\(\widehat{BCE}\) chung
Do đó: ΔBEC\(\sim\)ΔADC
Suy ra: \(\dfrac{EC}{DC}=\dfrac{CB}{CA}\)
hay \(CE\cdot CA=CB\cdot CD\left(1\right)\)
Xét ΔBMC vuông tại M có MD là đường cao ứng với cạnh huyền BC
nên \(CD\cdot CB=CM^2\left(2\right)\)
Xét ΔANC vuông tại N có NE là đường cao ứng với cạnh huyền AC
nên \(CN^2=CE\cdot CA\left(3\right)\)
Từ (1), (2) và (3) suy ra CM=CN
hay ΔCMN cân tại C