Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x (rupi) là giá tiền mỗi quả thanh yên.
Gọi y (rupi) là giá tiền mỗi quả táo rừng thơm.
Điều kiện x > 0, y > 0.
Mua 9 quả thanh yên và 8 quả táo rừng thơm hết 107 rupi
⇒ 9x + 8y = 107.
Mua 7 quả thanh yên và 7 quả táo rừng thơm là 91 rupi
⇒ 7x + 7y = 91 ⇔ x + y = 13.
Ta có hệ phương trình:
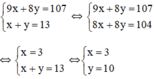
Vậy giá mỗi quả thanh yên là 3 rupi và mỗi quả táo rừng thơm là 10 rupi.

Gọi x (rupi) là giá tiền mỗi quả thanh yên.
Gọi y (rupi) là giá tiền mỗi quả táo rừng.
Điều kiện x > 0, y > 0.
Ta có hệ phương trình:
Giải ra ta được x = 3, y = 10.
Vậy, thanh yên 3 rupi/quả
táo rừng 10 rupi/quả.

c, Mình không vẽ được hình nên bạn thông cảm Gọi tâm đường tròn ngoại tiếp tam giác CME là K
Từ câu b : AM^2=AE.AC
Mà AC là cát tuyến của đường tròn ngoại tiếp tam giác CME
=> AM là tiếp tuyến của đường tròn ngoại tiếp tam giác CME
=> \(AM\perp MK\)
Mà \(AM\perp MB\)
=> M,K,B thẳng hàng
=> \(K\in MB\)cố định
Khi đó để NKmin thì K là hình chiếu của N lên MB
Đến đây bạn tự tính NK nhé
Sau đó từ MK để xác định điểm C

c)
5. Theo trên: \(\widehat{AMN}=\widehat{ACM}\)
=> AM là tiếp tuyến của đường tròn ngoại tiếp \(\Delta\) ECM;
Nối MB ta có\(\widehat{AMB}\)= 900 , do đó tâm O1 của đường tròn ngoại tiếp\(\Delta\)ECM phải nằm trên BM
. Ta thấy NO1 nhỏ nhất khi NO1 là khoảng cách từ N đến BM => NO1 \(\perp\)BM.
Gọi O1 là chân đường vuông góc kẻ từ N đến BM ta được:
O1 là tâm đường tròn ngoại tiếp D ECM có bán kính là O1M.
Do đó để khoảng cách từ N đến tâm đường tròn ngoại tiếp tam giác CME là nhỏ nhất thì C phải là giao điểm của đường tròn tâm O1 bán kính O1M với đường tròn (O) trong đó O1 là hình chiếu vuông góc của N trên BM.

x = tiền mua 1 quả thanh yên; y = .....táo
9x+8y = 107 (1)
7x+7y = 91 (2)
từ(1) và(2) giải x= 3; y = 10