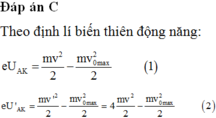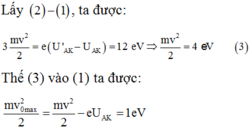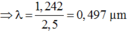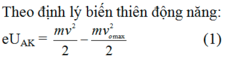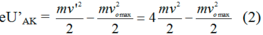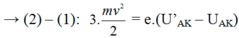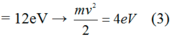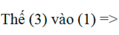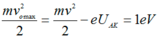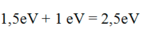Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng: \(\varepsilon=A_t+W_đ\)
Năng lượng \(\varepsilon\) tỉ lệ nghịch với bước sóng
Động năng Wđ tỉ lệ thuận với bình phương vận tốc v
Suy ra:
\(\varepsilon =A_t+W_đ\)(1)
\(\dfrac{\varepsilon}{2} =A_t+\dfrac{W_đ}{k^2}\)(2)
\(\dfrac{\varepsilon}{4} =A_t+\dfrac{W_đ}{10^2}\)(3)
Lấy (1) trừ (2) vế với vế: \(\dfrac{\varepsilon}{2} =(1-\dfrac{1}{k^2})W_đ\)(4)
(1) trừ (3):\(\dfrac{3\varepsilon}{4} =\dfrac{99}{100}W_đ\)(5)
Lấy (4) chia (5) vế với vế: \(\dfrac{2}{3}=(1-\dfrac{1}{k^2}).\dfrac{99}{100}\)
\(\Rightarrow k=\sqrt{\dfrac{200}{97}}\)

Gọi năng lượng bước sóng chiếu vào là \(\varepsilon\)
\(\Rightarrow\varepsilon=A_t+W_đ\)
Động năng của e khi đập vào anot là \(W_đ'\)
\(\Rightarrow W_đ'-W_đ=eU_{AK}\Rightarrow W_đ'=W_đ+eU_{AK}=\varepsilon-A_t+eU_{AK}\)
Từ đó suy ra: \(\frac{\varepsilon-A_t+eU_{AK1}}{\varepsilon-A_t+eU_{AK2}}=\frac{v_1^2}{v_2^2}=\frac{1}{4}\)
Thay số vào bạn sẽ tìm đc \(\varepsilon\)
Từ đó suy ra \(\lambda\)

Đáp án: B
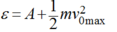
vomax là vận tốc lớn nhất của electrong khi bức ra khỏi K.
Khi ra khỏi K, dưới tác dụng của UAK thì electron tăng tốc chạy về A với vận tốc v được xác định bởi định lý động năng:
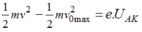
Hay:
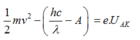
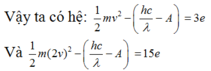
Nhân hai vế phương trình đầu cho 4, rồi lấy phương trình 2 trừ cho phương trình đầu ta được:
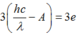
=> ![]()

câu hỏi của bn có ở đây nhá Câu hỏi của HOC24 - Học và thi online với HOC24

Ta có
Wđ= \(\frac{hc}{\lambda}\)
lấy tỉ lệ
1,5=\(\frac{hc}{1.2\lambda}\) => \(\lambda\)
sau đó A=\(\frac{hc}{\lambda}\)
không biết có đúng không. Nếu sai sót mong mn góp ý ạ![]()

Hệ thức Anh -xtanh
\(hf = A+ W_{đ max}\)
=> \(hf = 2,5 +1,5= 4 eV = 4.1,6.10^{-16}J.\)
=> \(\lambda = \frac{hc}{4.1,6.10^{-19}}= \frac{6,625.10^{-34}.3.10^8}{4.1,6.10^{-19}}=0,31 \mu m.\)