NT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
15 tháng 1 2024
\(a,-\dfrac{5}{7}+1+\dfrac{30}{-7}\le x\le-\dfrac{1}{6}+\dfrac{1}{3}+\dfrac{5}{6}\\ \dfrac{-5+1.7-30}{7}\le x\le\dfrac{-1+1.2+5}{6}\\ -\dfrac{28}{7}\le x\le\dfrac{6}{6}\\ -4\le x\le1\\ Vậy:x\in\left\{-4;-3;-2;-1;0;1\right\}\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
15 tháng 1 2024
\(b,\dfrac{-8}{13}+\dfrac{7}{17}+\dfrac{21}{13}\le x\le-\dfrac{9}{14}+3+\dfrac{5}{-14}\\ \left(\dfrac{21}{13}-\dfrac{8}{13}\right)+\dfrac{7}{17}\le x\le\left(-\dfrac{9}{14}-\dfrac{5}{14}\right)+3\\ 1+\dfrac{7}{17}\le x\le-1+3\\ 1\dfrac{7}{17}\le x\le2\\ Vậy:x=2\)
AH
Akai Haruma
Giáo viên
15 tháng 1 2024
Lời giải:
$\frac{1}{50}> \frac{1}{100}$
$\frac{1}{51}> \frac{1}{100}$
.....
$\frac{1}{98}> \frac{1}{100}$
$\frac{1}{99}> \frac{1}{100}$
$\Rightarrow S> \underbrace{\frac{1}{100}+\frac{1}{100}+...+\frac{1}{100}}_{50}=\frac{1}{100}.50=\frac{1}{2}$
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
15 tháng 1 2024
\(\left(3+3^2+3^3+3^4+...+3^{99}+3^{100}\right)\\ =3.\left(1+3\right)+3^3\left(1+3\right)+...+3^{99}\left(1+3\right)\\ =3.4+3^3.4+...+3^{99}.4\\ =4.\left(3+3^3+...+3^{99}\right)⋮4\left(ĐPCM\right)\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
24 tháng 1 2024
\(\dfrac{15}{34}+\dfrac{1}{3}+\dfrac{19}{34}-\dfrac{4}{3}+\dfrac{3}{7}=\left(\dfrac{15}{34}+\dfrac{19}{34}\right)+\left(\dfrac{1}{3}-\dfrac{4}{3}\right)+\dfrac{3}{7}=1-1+\dfrac{3}{7}=\dfrac{3}{7}\)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 1 2024
\(\dfrac{1}{n\left(n+1\right)}=\dfrac{1+n-n}{n\left(n+1\right)}=\dfrac{n+1}{n\left(n+1\right)}-\dfrac{n}{n\left(n+1\right)}=\dfrac{1}{n}-\dfrac{1}{n+1}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
29 tháng 1 2024
Bài 2:
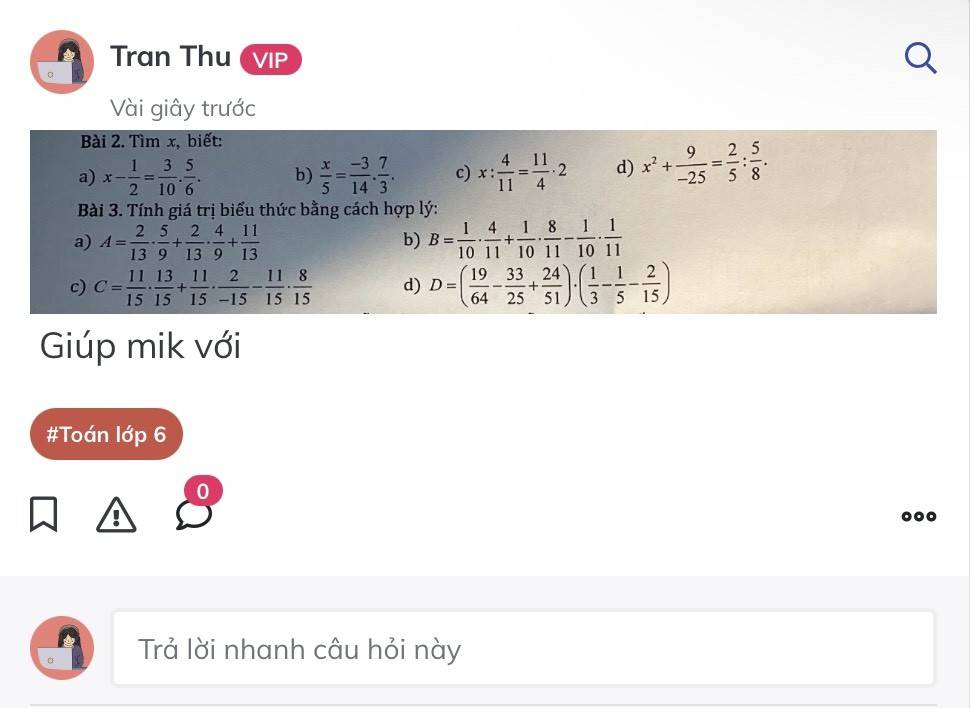
a; \(x\) - \(\dfrac{1}{2}\) = \(\dfrac{3}{10}\).\(\dfrac{5}{6}\)
\(x\) - \(\dfrac{1}{2}\) = \(\dfrac{1}{4}\)
\(x\) = \(\dfrac{1}{4}\) + \(\dfrac{1}{2}\)
\(x\) = \(\dfrac{3}{4}\)
Vậy \(x\) = \(\dfrac{3}{4}\)
b; \(\dfrac{x}{5}\) = \(\dfrac{-3}{14}\) \(\times\) \(\dfrac{7}{3}\)
\(\dfrac{x}{5}\) = \(\dfrac{-1}{2}\)
\(x\) = \(\dfrac{-1}{2}\) \(\times\) 5
\(x\) = \(\dfrac{-5}{2}\)
Vậy \(x\) = \(\dfrac{-5}{2}\);
c; \(x\) : \(\dfrac{4}{11}\) = \(\dfrac{11}{4}\) \(\times\) 2
\(x\) : \(\dfrac{4}{11}\) = \(\dfrac{11}{2}\)
\(x\) = \(\dfrac{11}{2}\) \(\times\) \(\dfrac{4}{11}\)
\(x\) = 2
Vậy \(x\) = 2
d; \(x^2\) + \(\dfrac{9}{-25}\) = \(\dfrac{2}{5}\) : \(\dfrac{5}{8}\)
\(x^2\) - \(\dfrac{9}{25}\) = \(\dfrac{16}{25}\)
\(x^2\) = \(\dfrac{16}{25}\) + \(\dfrac{9}{25}\)
\(x^2\) = \(\dfrac{25}{25}\)
\(x^2\) = 1
\(\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)
Vậy \(x\)\(\in\) {-1; 1}
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
29 tháng 1 2024
Bài 3:
a; A = \(\dfrac{2}{13}\)\(\times\) \(\dfrac{5}{9}\)+ \(\dfrac{2}{13}\)\(\times\)\(\dfrac{4}{9}\) + \(\dfrac{11}{13}\)
A = \(\dfrac{2}{13}\) \(\times\)(\(\dfrac{5}{9}\) + \(\dfrac{4}{9}\)) + \(\dfrac{11}{13}\)
A = \(\dfrac{2}{13}\) \(\times\) \(\dfrac{9}{9}\) + \(\dfrac{11}{13}\)
A = \(\dfrac{2}{13}\) + \(\dfrac{11}{13}\)
A = 1
b; B = \(\dfrac{1}{10}\).\(\dfrac{4}{11}\) + \(\dfrac{1}{10}\).\(\dfrac{8}{11}\) - \(\dfrac{1}{10}\).\(\dfrac{1}{11}\)
B = \(\dfrac{1}{10}\) x (\(\dfrac{4}{11}\) + \(\dfrac{8}{11}\) - \(\dfrac{1}{11}\))
B = \(\dfrac{1}{10}\) x (\(\dfrac{12}{11}\) - \(\dfrac{1}{11}\))
B = \(\dfrac{1}{10}\) x \(\dfrac{11}{11}\)
B = \(\dfrac{1}{10}\)
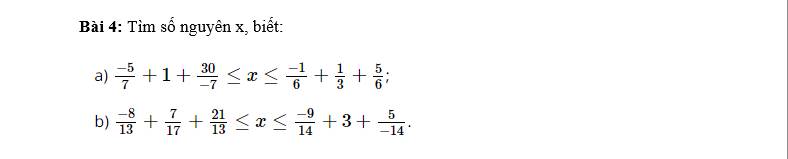
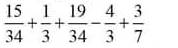
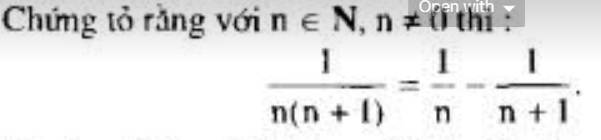
z4:
\(\dfrac{24}{148}=\dfrac{6}{37}=\dfrac{108}{37\cdot18}\)
\(\dfrac{-14}{-36}=\dfrac{7}{18}=\dfrac{7\cdot37}{18\cdot37}=\dfrac{259}{37\cdot18}\)
mà 108<259
nên \(\dfrac{24}{148}< \dfrac{-14}{-36}\)
z5: \(\dfrac{-26}{-72}=\dfrac{26}{72}< 1\)
\(1< \dfrac{45}{20}=\dfrac{-45}{-20}\)
Do đó: \(\dfrac{-26}{-72}< \dfrac{-45}{-20}\)
z6: \(\dfrac{14}{42}=\dfrac{1}{3}=\dfrac{1\cdot4}{3\cdot4}=\dfrac{4}{12}\)
\(\dfrac{21}{28}=\dfrac{3}{4}=\dfrac{3\cdot3}{4\cdot3}=\dfrac{9}{12}\)
mà 4<9
nên \(\dfrac{14}{42}< \dfrac{21}{28}\)
z7: \(\dfrac{-14}{-56}=\dfrac{1}{4}=\dfrac{5}{20}\)
\(\dfrac{21}{35}=\dfrac{3}{5}=\dfrac{3\cdot4}{5\cdot4}=\dfrac{12}{20}\)
mà 5<12
nên \(\dfrac{-14}{-56}< \dfrac{21}{35}\)
z8: \(10A=\dfrac{10^{201}+10}{10^{201}+1}=1+\dfrac{9}{10^{201}+1}\)
\(10B=\dfrac{10^{202}+10}{10^{202}+1}=1+\dfrac{9}{10^{202}+1}\)
\(10^{201}+1< 10^{202}+1\)
=>\(\dfrac{9}{10^{201}+1}>\dfrac{9}{10^{202}+1}\)
=>\(\dfrac{9}{10^{201}+1}+1>\dfrac{9}{10^{202}+1}+1\)
=>10A>10B
=>A>B