MH
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
17 tháng 4 2017
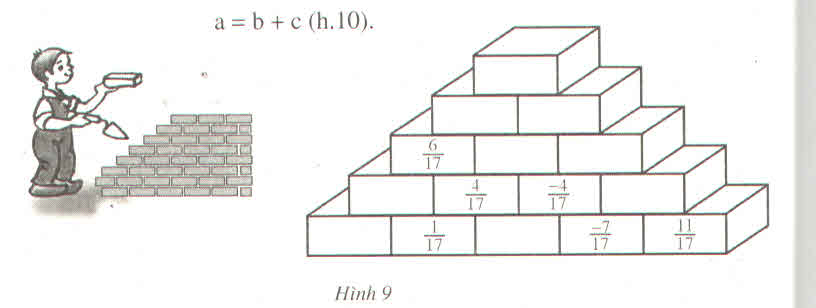
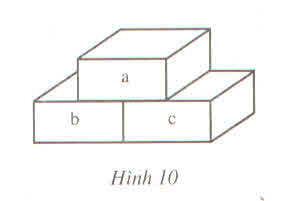
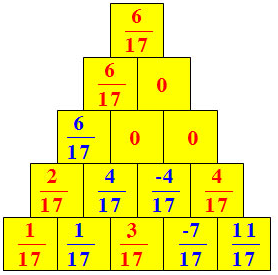
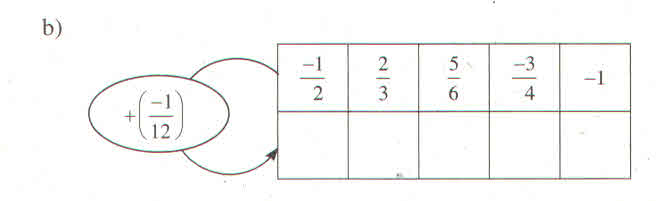
Làm theo quy tắc ở hình 10, ta có thể "xây tường" như sau:
SG
3
18 tháng 4 2017
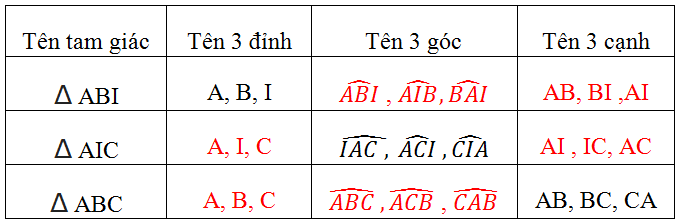
Giải:
|
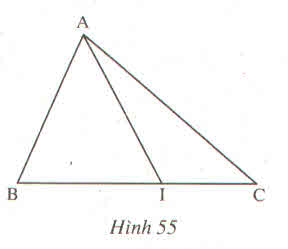
Tên tam giác |
Tên 3 đỉnh |
Tên 3 góc |
Tên 3 cạnh |
|
|
A,B,I |
|
AB, BI, IA |
|
|
A,I,C |
|
AI, IC, CA |
|
|
A,B,C |
|
AB, BC, CA |
SG
2
18 tháng 4 2017
Hướng dẫn vẽ:
a) Trước hết vẽ đường tròn bán kính 1.2 cm rồi vẽ đường kình của đường tròn. Trên hai nửa mặt phẳng bờ đối nhau là đường kính vẽ hai nửa đường tròn có đường kính lần lượt là đoạn nối tâm tới một đầu của đường kính vừa vẽ. Sau cùng tô màu như hình vẽ.
b) Trước hết, vẽ hình vuông. Lấy giao điểm của hai đường chéo làm tâm vẽ 5 đường tròn có bán kính lần lượt bằng bán kính của 5 đường tròn đã cho.
c) Trước hết vẽ đường tròn ở chính giữa có bán kình R. Vẽ một đường tròn phụ trùng với tâm đường tròn vừa vẽ, bán kính 2 R. Trên đường tròn phụ, vẽ liên tiếp 6 dây, mỗi dây có độ dài 2R .Sau đó vẽ sáu đường tròn có tâm là mút của mỗi dây.
d) Vẽ đường tròn bán kính R bằng bán kình của đường tròn ở chính giữa. Vẽ liên tiếp sáu dây, mỗi dây dài R. Vẽ sáu nửa đường tròn ra phía ngoài của đường tròn vừa vẽ mỗi nửa đường tròn có đường kính là mỗi dây.
TT
18 tháng 4 2017
Sách Giáo Khoa
Cách vẽ:
Hình a) Trước hết vẽ đường tròn bán kính 1,2 cm rồi vẽ đường kính của đường tròn. Trên hai nửa mặt phẳng bờ đối nhau là đường kính vẽ hai nửa đường tròn có đường kính lần lượt là đoạn nối tâm tới một đầu của đường kính vừa vẽ. Sau cùng tô màu như hình vẽ.
Hình b) Trước hết, vẽ hình vuông. Lấy giao điểm của hai đường chéo làm tâm vẽ 5 đường tròn có bán kính lần lượt bằng bán kính của 5 đường tròn đã cho.
SG
1
18 tháng 4 2017
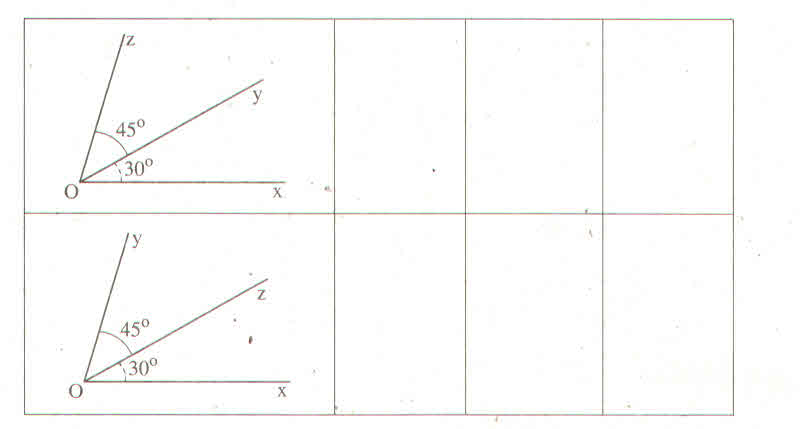
Giải:
|
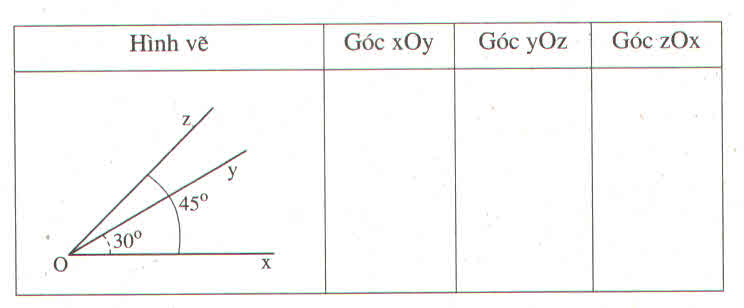
Hình |
Tên góc (cách viết thông thường) |
Tên đỉnh |
Tên cạnh |
Tên góc (Cách viết kí hiệu) |
|
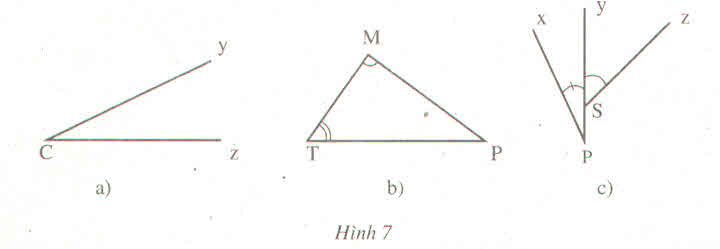
a |
Góc yCz, góc zCy, góc C |
C |
Cy,Cz |
|
|
b |
Góc MTP, PTM, T Góc TMP, PMT,M Góc TPM, MPT,P |
T M P |
TM,TP MT,MP PT,PM |
|
|
c |
Góc xPy,yPx,P Góc ySz,zSy |
P S |
Px, Py Sy, Sz |
|
SG
2
10 tháng 6 2017
Kết quả tìm được đúng
Phương pháp này không thể áp dụng để rút gọn các phân số có dạng \(\dfrac{\overline{ab}}{\overline{bc}}\)
VD: Phân số \(\dfrac{26}{64}\) có dạng \(\dfrac{\overline{ab}}{\overline{bc}}\) nhưng khi rút gọn thì được phân số \(\dfrac{13}{32}\) , chứ không phải phân số \(\dfrac{1}{2}\) theo phương pháp trên ta có được.
Hoặc là phân số \(\dfrac{18}{88}\) có dạng \(\dfrac{\overline{ab}}{\overline{bc}}\) nhưng khi rút gọn thì được phân số \(\dfrac{9}{44}\) , chứ không phải phân số \(\dfrac{1}{8}\) theo phương pháp trên ta có được.
6 tháng 5 2018
Kiểm tra ta thấy các kết quả tìm được đều đúng. Tuy nhiên, không thể áp dụng "phương pháp" trên để rút gọn các phân số có dạng ab/bc.
Ví dụ : 
Cách "rút gọn" của bạn Minh chỉ đúng một cách ngẫu nhiên
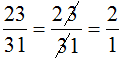
a, Vì các chữ số tận cùng đều là số chẵn nên kết quả là chẵn => chia hết cho 2
b, Vì các chữ số tận cùng là 0 và 5 nên kết quả sẽ ra số tận cùng là 0 hoặc 5 => chia hết cho 5
a,Vì 61782:2,94656:2,76320:2
➜61782+94656-76320 chia hết cho2
b,Như câu a