
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


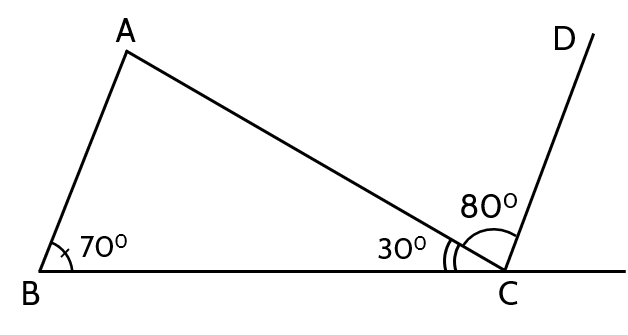
Xét tg ABC có
\(\widehat{BAC}=180^o-\widehat{ABC}-\widehat{ACB}\) (tổng các góc trong của 1 tg \(=180^o\) )
\(\Rightarrow\widehat{BAC}=180^o-70^o-30^o=80^o=\widehat{ACD}\)
Hai góc \(\widehat{BAC}=\widehat{ACD}\) ở vị trí so le trong => AB//CD

3. Xét tam giác ADM và tam giác AEM có :
góc ADM = góc AEM = 90 độ
Góc BAM = góc CAM (gt)
AM chung
=>Tam giác ADM = tam giác AEm (c.huyền - g.nhọn)
=>MD = ME (cặp cạnh t/ứng )
AD = AE (cặp cạnh t/ứng )
Xét tam giác MDB và tam giác MEC có :
MB = MC (gt)
góc MDB = góc MEC = 90 độ
MD = ME ( câu a)
=>Tam giác MDB = Tam giác MEC (c.huyền-c.g.vuông)
Vì AD + DB = AB
AE + EC = AC
Mà AD = AE
DB = EC
=>AB = AC
Xét tam giác ABM và tam giác ACM có
AM chung
góc BAM = góc CAM (gt)
AB = AC (CMT)
=>Tam giác ABM = Tam giác ACM (c.huyền-g.nhon)
Vậy có 3 cặp tam giác bằng nhau

Xét ∆ABC và ∆DBC có:
AB = BD
Góc ABC = góc CBD
Góc BAC = góc BDC
=> ∆ABC = ∆DBC

a/
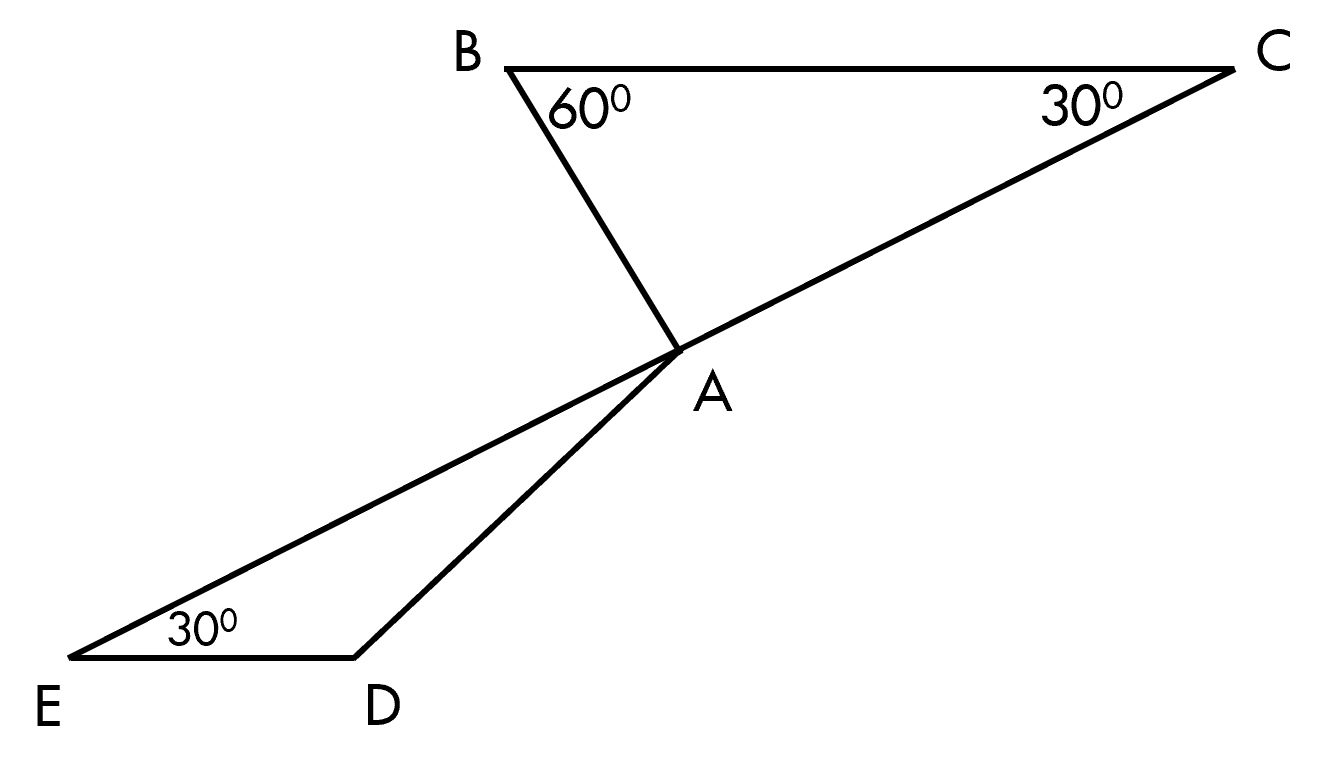
\(\widehat{BCE}=\widehat{CED}=30^o\)
Hai góc trên ở vị trí sole trong => BC//DE
b/
Ta có
BC//DE (cmt) \(\Rightarrow\widehat{AFB}=180^o-\widehat{EDF}\) (Hai góc trong cùng phía bù nhau)
\(\Rightarrow\widehat{AFB}=180^o-135^o=45^o\)

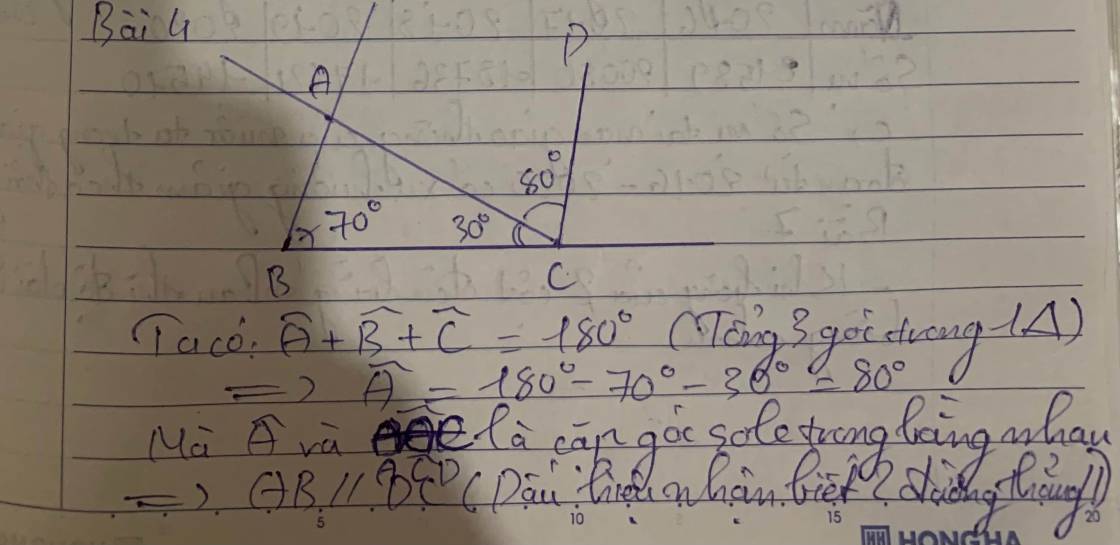

 M.n giải hộ em vs đg cần gấp ạ
M.n giải hộ em vs đg cần gấp ạ
a. xét ΔABH và ΔACH, có:
AB = AC (ΔABC cân tại A)
\(\widehat{ABC}=\widehat{ACB}\left(\text{Δ}ABC\text{ cân tại A}\right)\)
HB = HC (H là trung điểm BC)
=> ΔABH = ΔACH (c-g-c)
b. trong ΔABC cân tại A có AH là đường trung tuyến
=> AH cũng là đường phân giác
\(=>\widehat{DAH}=\widehat{EAH}\) (1)
xét Δ vuông DAH và Δ vuông EAH có:
AH là cạnh chung; \(\widehat{DAH}=\widehat{EAH}\) (từ (1))
=> Δ DAH = Δ EAH (ch-gn)
=> HD = HE (2 cạnh tương ứng)
=> ΔHDE là Δ cân (tại H)
c. ta có Δ DAH = Δ EAH (câu b)
=> AD = AE (2 cạnh tương ứng)
=> ΔDEA là Δ cân tại A
xét ΔDEA cân tại A có: \(\widehat{ADE}=\dfrac{180^0-\widehat{A}}{2}\left(2\right)\)
xét ΔABC cân tại A có: \(\widehat{ABC}=\dfrac{180^0-\widehat{A}}{2}\left(3\right)\)
từ (2) và (3) => \(\widehat{ADE}=\widehat{ABC}\)
mà 2 góc này ở vị trí đồng vị
=> DE // BC