Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lấy điểm O cố định rồi đặt \(\overrightarrow{OA_1}=\overrightarrow{a_1};\overrightarrow{OB_1}=\overrightarrow{b_1};\overrightarrow{OC_1}=\overrightarrow{c_1};\overrightarrow{OD_1}=\overrightarrow{d_1}\)
Điều kiện cần và đủ để tứ giác \(A_1B_1C_1D_1\) là hình bình hành là :
\(\overrightarrow{a_1}+\overrightarrow{c_1}=\overrightarrow{b_1}+\overrightarrow{d_1}\) (1)
\(\overrightarrow{a}+\overrightarrow{c}=\overrightarrow{b}+\overrightarrow{d}\Leftrightarrow\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{OB}+\overrightarrow{OD}\)
<=> Tứ giác ABCD là hình bình hành

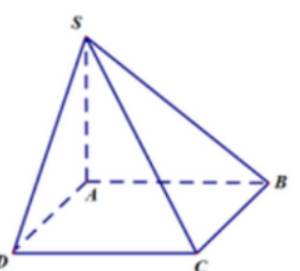
Hình chóp S.ABCD có các mặt bên là hình tam giác nên hình biểu diễn của nó cũng có các mặt bên là hình tam giác.
ABCD là hình bình hành nên hình biểu diễn của nó cũng là hình bình hành
Từ đó, ta vẽ được hình biểu diễn của hình chóp S.ABCD

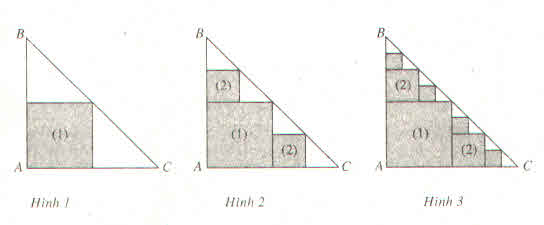
a) Hình vuông thứ nhất có cạnh bằng nên u1 = (
)2 =
.
Hình vuông thứ hai có cạnh bằng nên u2 = (
)2 =
.
Hình vuông thứ ba có cạnh bằng nên u3 = (
)2 =
.
Tương tự, ta có un =
b) Dãy số (un) là một cặp số nhân lùi vô hạn với u1 = và q =
. Do đó
lim Sn = .

a.
Ta có: \(\begin{cases}S\in\left(SAB\right)\cap\left(SCD\right)\\ AB\Vert CD\\ AB\subset\left(SAB\right);CD\subset\left(SCD\right)\end{cases}\)
\(\Rightarrow\left(SAB\right)\cap\left(SCD\right)=Sx\Vert AB\Vert CD\)
b.
Gọi O là giao điểm AC và BD =>O là trung điểm AC và BD
\(O\in AC\subset\left(IAC\right)\Rightarrow IO\subset\left(IAC\right)\)
O là trung điểm BD, I là trung điểm SD =>OI là đường trung bình tam giác SBD
=>OI song song SB
Ta có: \(\begin{cases}C\in\left(IAC\right)\cap\left(SBC\right)\\ OI\Vert SB\\ OI\subset\left(IAC\right);SB\subset\left(SBC\right)\end{cases}\) \(\Rightarrow\left(IAC\right)\cap\left(SBC\right)=Cx\Vert SB\)
Đề bài:
Cho hình chóp \(S . A B C D\) có đáy là hình bình hành.
- Tìm giao tuyến của mặt phẳng \(\left(\right. S A B \left.\right)\) và mặt phẳng \(\left(\right. S C D \left.\right)\).
- Gọi \(I\) là trung điểm của \(S D\). Mặt phẳng \(\left(\right. I A C \left.\right)\) và mặt phẳng \(\left(\right. S B C \left.\right)\) cắt nhau theo giao tuyến \(C x\). Chứng minh rằng \(C x \parallel S B\).
Phần a) Tìm giao tuyến của mặt phẳng \(\left(\right. S A B \left.\right)\) và mặt phẳng \(\left(\right. S C D \left.\right)\):
1. Mô tả các mặt phẳng:
- Mặt phẳng \(\left(\right. S A B \left.\right)\) là mặt phẳng chứa các điểm \(S\), \(A\), và \(B\).
- Mặt phẳng \(\left(\right. S C D \left.\right)\) là mặt phẳng chứa các điểm \(S\), \(C\), và \(D\).
2. Tính giao tuyến của hai mặt phẳng:
Hai mặt phẳng này có giao tuyến là một đường thẳng, và để tìm giao tuyến này, ta cần tìm một điểm chung của hai mặt phẳng và một hướng của đường thẳng giao tuyến.
- Mặt phẳng \(\left(\right. S A B \left.\right)\) chứa các điểm \(S\), \(A\), và \(B\).
- Mặt phẳng \(\left(\right. S C D \left.\right)\) chứa các điểm \(S\), \(C\), và \(D\).
Lưu ý rằng điểm \(S\) là chung của cả hai mặt phẳng. Giao tuyến của hai mặt phẳng này sẽ là đường thẳng đi qua điểm \(S\)và vuông góc với các cạnh của đáy \(A B C D\) tại các điểm \(A\), \(B\), \(C\), và \(D\).
Do đáy \(A B C D\) là hình bình hành, các cạnh đối diện của hình bình hành sẽ song song. Do đó, giao tuyến của hai mặt phẳng \(\left(\right. S A B \left.\right)\) và \(\left(\right. S C D \left.\right)\) chính là đoạn thẳng nối giữa hai điểm \(B\) và \(C\) trong không gian.
Kết luận: Giao tuyến của hai mặt phẳng \(\left(\right. S A B \left.\right)\) và \(\left(\right. S C D \left.\right)\) là đoạn thẳng \(B C\).
Phần b) Chứng minh \(C x \parallel S B\):
1. Mô tả các mặt phẳng:
- \(I\) là trung điểm của đoạn \(S D\), nghĩa là \(I\) chia đoạn \(S D\) thành hai phần bằng nhau.
- Mặt phẳng \(\left(\right. I A C \left.\right)\) chứa các điểm \(I\), \(A\), và \(C\).
- Mặt phẳng \(\left(\right. S B C \left.\right)\) chứa các điểm \(S\), \(B\), và \(C\).
Cả hai mặt phẳng này giao nhau tại đường thẳng \(C x\), và chúng ta cần chứng minh rằng đường thẳng \(C x\) song song với \(S B\).
2. Tính chất của các mặt phẳng:
- Mặt phẳng \(\left(\right. I A C \left.\right)\) và mặt phẳng \(\left(\right. S B C \left.\right)\) cắt nhau theo đường thẳng \(C x\).
- Do \(I\) là trung điểm của \(S D\), ta có \(S I = I D\). Vì vậy, \(I\) chia đoạn \(S D\) thành hai phần bằng nhau.
- Mặt phẳng \(\left(\right. I A C \left.\right)\) đi qua \(I\), \(A\), và \(C\), còn mặt phẳng \(\left(\right. S B C \left.\right)\) đi qua \(S\), \(B\), và \(C\).
3. Chứng minh tính song song:
- Ta có thể áp dụng các tính chất về đường thẳng và mặt phẳng song song trong không gian.
- Vì \(I\) là trung điểm của \(S D\), và \(C x\) là giao tuyến của hai mặt phẳng \(\left(\right. I A C \left.\right)\) và \(\left(\right. S B C \left.\right)\), ta nhận thấy rằng đường thẳng \(C x\) phải song song với đường thẳng \(S B\) do tính chất của các mặt phẳng giao nhau tại điểm \(C x\).
Cụ thể, vì hai mặt phẳng \(\left(\right. I A C \left.\right)\) và \(\left(\right. S B C \left.\right)\) có một điểm chung là \(C\) và đường thẳng \(C x\) là giao tuyến của chúng, mà mặt phẳng \(\left(\right. S B C \left.\right)\) chứa \(S B\), do đó \(C x\) sẽ song song với \(S B\).
Kết luận: Đường thẳng \(C x\) song song với \(S B\), tức là \(C x \parallel S B\).
Tóm lại:
- Giao tuyến của mặt phẳng \(\left(\right. S A B \left.\right)\) và mặt phẳng \(\left(\right. S C D \left.\right)\) là đoạn thẳng \(B C\).
- Đường thẳng giao tuyến \(C x\) của hai mặt phẳng \(\left(\right. I A C \left.\right)\) và \(\left(\right. S B C \left.\right)\) song song với \(S B\), tức là \(C x \parallel S B\).

Chọn B.
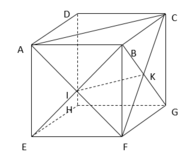
- Ta có:
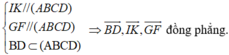
- + Các bộ véctơ ở phương án A, C, D không thể có giá cùng song song với một mặt phẳng.

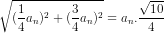 với n ε N*.
với n ε N*. 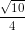

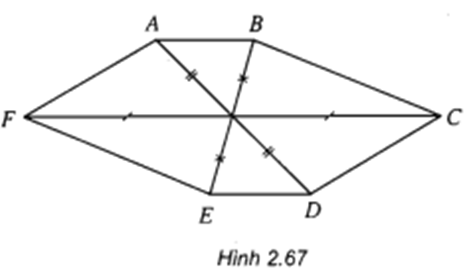


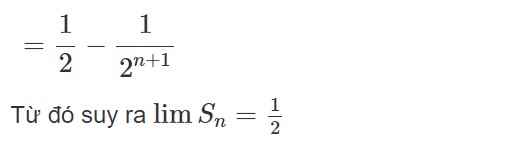
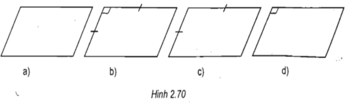
Hình 2.70a biểu diễn hình bình hành
Hình 2.70b biểu diễn hình vuông
Hình 2.70c biểu diễn hình thoi
Hình 2.70d biểu diễn hình chữ nhật