Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Năng lượng liên kết riêng của các hạt được tính theo công thức sau:
\(\varepsilon=\dfrac{W_{lk}}{A}\) nên ta có:
\(\varepsilon_{^2H}=\dfrac{2,22}{2}=1,11MeV\)
\(\varepsilon_{^3H}=\dfrac{8,49}{3}=2,83MeV\)
\(\varepsilon_{^4He}=\dfrac{28,16}{4}=7,04MeV\)
\(\Rightarrow\varepsilon_{He}>\varepsilon_{^3H}>\varepsilon_{^2H}\)
Chọn C.

+ Độ bền vững của hạt nhân được xét dựa trên năng lượng liên kết riêng: ![]()
+ ![]() có Wlkr = 1,11 MeV;
có Wlkr = 1,11 MeV; ![]() có Wlkr = 2,83 MeV;
có Wlkr = 2,83 MeV; ![]() có Wlkr = 7,04 MeV.
có Wlkr = 7,04 MeV.
→ Độ bền vững hạt nhân sắp xếp theo thứ tự giảm dần là: ![]()
-
Đáp án C

\(W_{lkr}= \frac{W_{lk}}{A}\)
Năng lượng liên kết riêng của \(_1^2H\), \(_1^3H\), \(_2^4He\) lần lượt là 1,11 MeV; 2,83 MeV; 7,04 MeV.
Hạt nhân có năng lượng liên kết riêng càng lớn thì càng bền vững
=> Thứ tự giảm dẫn về độ bền vững là \(_2^4He\), \(_1^3H\), \(_1^2H\).

\(m_t = m_{Na}+ m_H = 22,9837+ 1,0073 = 23,991u.\)
\(m_s = m_{He}+ m_{Ne} = 19,9869+ 4,0015 = 23,9884u.\)
=> \(m_t > m_s\), phản ứng là tỏa năng lượng.
Năng lượng tỏa ra là
\(E = (m_t-m_s)c^2 = 2,6.10^{-3}uc^2 = 2,6.10^{-3}.931,5 = 2,4219 MeV.\)
CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCc



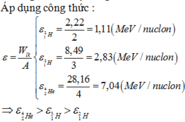
Chọn C