Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài giải:
a) Đúng.
Gọi O là trung điểm của AB. Ta có CO là trung tuyến ứng với cạnh huyền nên
OC = 1212AB hay OC = OA = OB. Nên A, B, C cùng thuộc đường tròn bán kình OA. Vậy C thuộc đường tròn đường kính AB.
b) Đúng.
Gọi O là tâm đường tròn. Tam giác ABC có trung tuyến CO bằng nửa cạnh AB (do CO = AO = OB) nên tam giác ABC vuông tại C.
a) Đúng.
Gọi O là trung điểm của AB. Ta có CO là trung tuyến ứng với cạnh huyền nên
OC = \(\dfrac{1}{2}\)AB hay OC = OA = OB. Nên A, B, C cùng thuộc đường tròn bán kình OA. Vậy C thuộc đường tròn đường kính AB.
b) Đúng.
Gọi O là tâm đường tròn. Tam giác ABC có trung tuyến CO bằng nửa cạnh AB (do CO = AO = OB) nên tam giác ABC vuông tại C.


a) △ AKB ~ △AIC (g - g) ( ˆK=ˆI=900;K^=I^=900;ˆAA^ chung) (3)
⇒ ˆACI=ˆABKACI^=ABK^
⇒ 900−ˆACI=900−ˆABK900−ACI^=900−ABK^
⇒ ˆHCD=ˆHBDHCD^=HBD^ (1)
xét tứ giác AKHI có
ˆKHI=3600−ˆA−ˆHKA−ˆHIA=1800−ˆAKHI^=3600−A^−HKA−^HIA^=1800−A^
tương tự ˆD=1800−ˆAD^=1800−A^
⇒ ˆKHI=ˆDKHI^=D^ (2)
từ (1) và (2) ⇒ BHCD là hình bình hành
b) từ (3) ⇒ AIAK=ACABAIAK=ACAB (4)
⇒ AI.AB = AK.AC
c) xét △AKI và △ABC có
ˆAA^ chung; (4)
⇒ △AKI ~ △ABC (c-g-c)
d) gọi K là giao của DH và BC
vì A,D,H thăng hàng và H là trực tâm nên AD ⊥ BC hay HD ⊥ BC
⇒ BDCH là hình thoi
⇒ KC = KB
⇒ △ ABK = △ ACK (c-g-c)
⇒ △ ABC cân tại A
vậy △ ABC cân tại A thì DH đi qua A và BHCD là hình thoi
nó bị lỗi mk gửi lại
a) △ AKB ~ △AIC (g - g) ( ˆK=ˆI=900,ˆAA^ chung) (3)
⇒ ˆACI=ˆABK
⇒ 900−ˆACI=900−ˆABK
⇒ ˆHCD=ˆHBD (1)
xét tứ giác AKHI có
ˆKHI=3600−ˆA−ˆHKA−ˆHIA=1800−ˆA
tương tự ˆD=1800−ˆAD^=1800−A^
⇒ ˆKHI=ˆD (2)
từ (1) và (2) ⇒ BHCD là hình bình hành
b) từ (3) ⇒ AI/AK=AC/AB (4)
⇒ AI.AB = AK.AC
c) xét △AKI và △ABC có
ˆAA^ chung; (4)
⇒ △AKI ~ △ABC (c-g-c)
d) gọi K là giao của DH và BC
vì A,D,H thăng hàng và H là trực tâm nên AD ⊥ BC hay HD ⊥ BC
⇒ BDCH là hình thoi
⇒ KC = KB
⇒ △ ABK = △ ACK (c-g-c)
⇒ △ ABC cân tại A
vậy △ ABC cân tại A thì DH đi qua A và BHCD là hình thoi
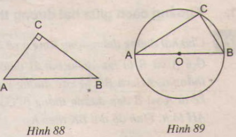
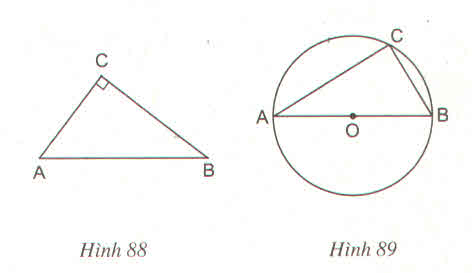
a) Đúng
Gọi O là trung điểm của AB.
Ta có CO là trung tuyến ứng với cạnh huyền nên
⇒ OC = AB/2 = OA = OB.
⇒ A, B, C cùng thuộc đường tròn bán kính OA.
Tâm O là trung điểm của AB nên AB là đường kính.
Vậy C thuộc đường tròn đường kính AB.
b) Đúng
Gọi O là tâm đường tròn.
⇒ OA = OB = OC = R
AB là đường kính nên AB = 2R.
Tam giác ABC có CO là trung tuyến và CO = AB/2
⇒ ΔABC vuông tại C.