Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
c: Để hai đường thẳng song song thì m-1=2
hay m=3

a.
Đặt \(\left\{{}\begin{matrix}\sqrt{x^2+2x+3}=a>0\\\sqrt{x^2+x+2}=b>0\end{matrix}\right.\) \(\Rightarrow a^2-b^2=x+1\)
Pt trở thành:
\(a+b=2\left(a^2-b^2\right)\)
\(\Leftrightarrow a+b=\left(2a-2b\right)\left(a+b\right)\)
\(\Leftrightarrow2a-2b=1\) (do \(a+b>0\))
\(\Leftrightarrow2a=2b+1\)
\(\Leftrightarrow2\sqrt{x^2+2x+3}=2\sqrt{x^2+x+2}+1\)
\(\Leftrightarrow4\left(x^2+2x+3\right)=4\left(x^2+x+2\right)+1+4\sqrt{x^2+x+2}\)
\(\Leftrightarrow4x+3=4\sqrt{x^2+x+2}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-\dfrac{3}{4}\\16\left(x^2+x+2\right)=\left(4x+3\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-\dfrac{3}{4}\\8x=23\end{matrix}\right.\) \(\Rightarrow x=\dfrac{23}{8}\)
b.
ĐKXĐ: \(x\ge3\)
Đặt \(\left\{{}\begin{matrix}\sqrt{x-3}=a\ge0\\\sqrt{x+2}=b>0\end{matrix}\right.\) \(\Rightarrow a^2-b^2=-5\)
Phương trình trở thành:
\(\left(a-b\right)\left(ab+1\right)=a^2-b^2\)
\(\Leftrightarrow\left(a-b\right)\left(ab+1\right)=\left(a-b\right)\left(a+b\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}a=b\left(vô-nghiệm\right)\\ab+1=a+b\end{matrix}\right.\)
\(\Rightarrow ab-a-b+1=0\)
\(\Leftrightarrow\left(a-1\right)\left(b-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}a=1\\b=1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x-3}=1\\\sqrt{x+2}=1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=4\\x=-1\left(ktm\right)\end{matrix}\right.\)

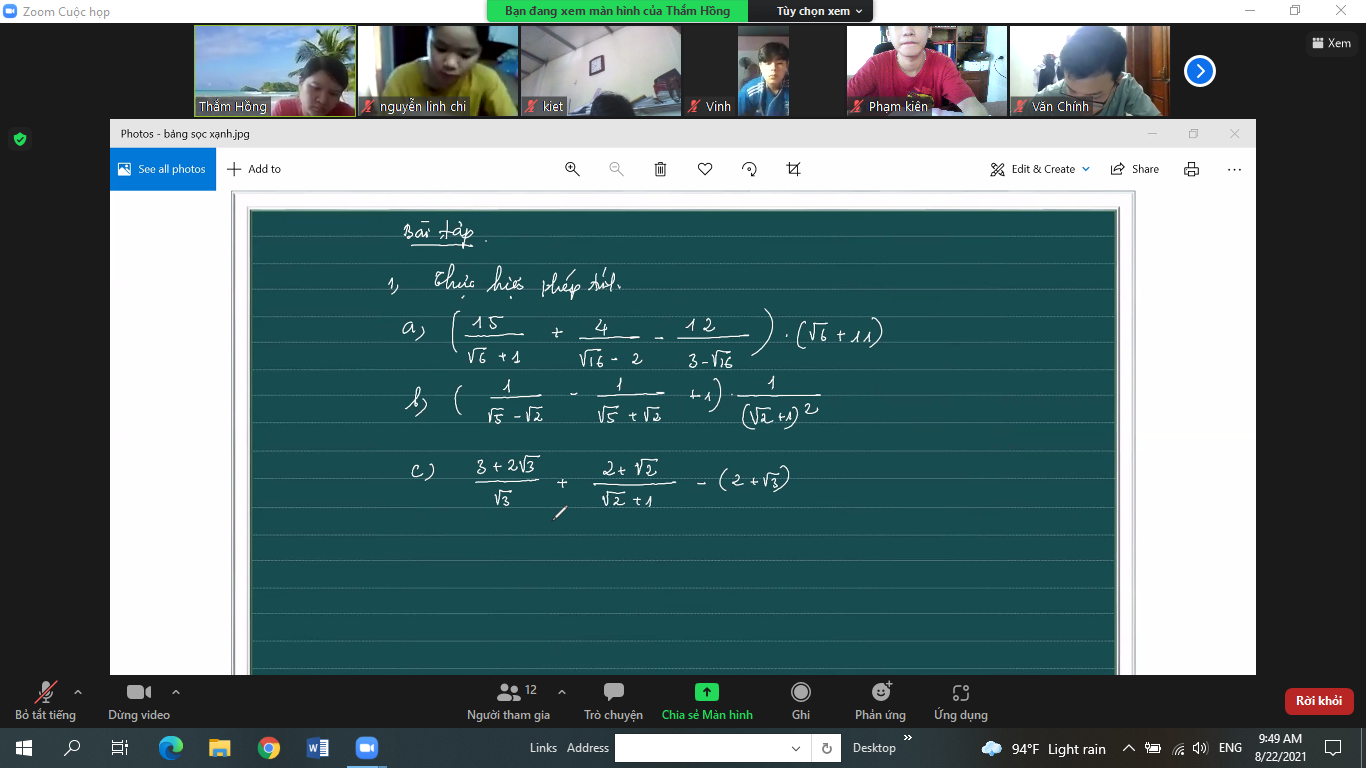
a)
=15(can6-1)/(6-1)+4/(4-2)-12/(3-4)
=3(can6-1)+2+12
=3\(\sqrt{6}\)-3+2+12
=17+3can6
các câu còn lại tương tự liên hợp mẫu


\(A=\dfrac{2a^2+4}{1-a^3}-\dfrac{1}{1+\sqrt{a}}-\dfrac{1}{1-\sqrt{a}}\\ =\dfrac{2a^2+4}{\left(1-a\right)\left(1+a+a^2\right)}-\dfrac{1}{1+\sqrt{a}}-\dfrac{1}{1-\sqrt{a}}\\ =\dfrac{2a^2+4-\left(1-\sqrt{a}\right)\left(1+a+a^2\right)-\left(1+\sqrt{a}\right)\left(1+a+a^2\right)}{\left(1-a\right)\left(1+a+a^2\right)}\\ =\dfrac{2a^2+4-\left(1+a+a^2\right)\left(1-\sqrt{a}+1+\sqrt{a}\right)}{\left(1-a\right)\left(1+a+a^2\right)}\\ =\dfrac{2a^2+4-2\left(1+a+a^2\right)}{\left(1-a\right)\left(1+a+a^2\right)}=\dfrac{2}{1+a+a^2}\\ \)
Ta có A max <=> \(1+a+a^2min\)
Mà 1+a+a^2=\(\left(a+\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\\ \)
Dấu bằng xảy ra <=> a=-1/2
=> \(A=\dfrac{2}{1+a+a^2}\le\dfrac{2}{\dfrac{3}{4}}=\dfrac{8}{3}\)
Vậy max A=8/3 <=> a=-1/2
=)) mỏi tay quá đê


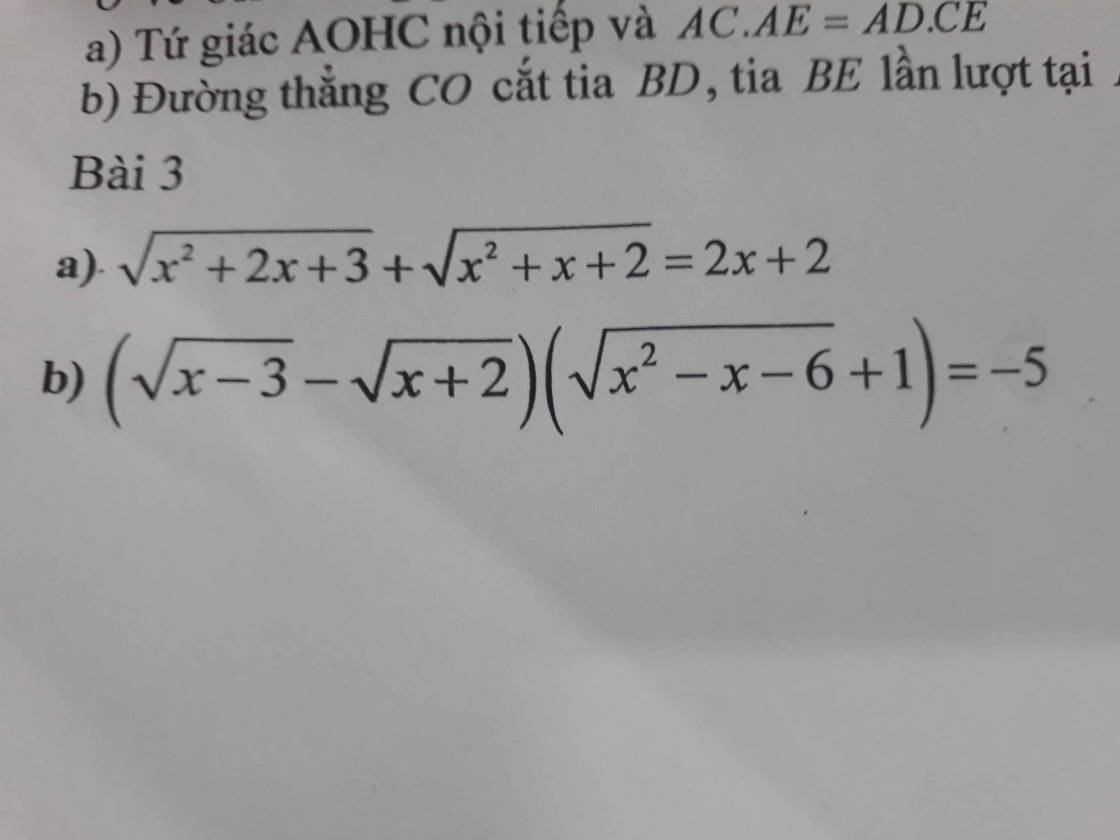


Bài 2,3,4 nhé
đâu