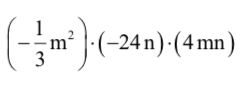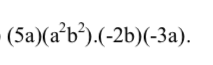Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(P\left(x\right)=3x^4+x^2-3x^4+5\\ =x^2+5\)
b) \(P\left(0\right)=0^2+5=5\\ P\left(-3\right)=\left(-3\right)^2+5=-9+5=4\)
c) Ta có: x2 ≥ 0 với mọi x
Nên x2 + 5 > 5 hay f(x) > 5
Vậy đa thức P(x) không có nghiệm
a) \(P\left(x\right)=x^2+5\)
b) \(P\left(0\right)=0^2+5=5\)
\(P\left(-3\right)=\left(-3\right)^2+5=14\)
c) Để P(x) có nghiệm
<=> \(P\left(x\right)=0\)
<=> \(x^2+5=0\)
<=> \(x^2=-5\) (vô lívì \(x^2\ge0\left(\forall x\right)\))
=> P(x) không có nghiệm

phân số thập phân là phân số có mẫu là 10; 100; 1000; ...
phân số thập phân này có tích tử và mẫu là 260 vậy, tử và mẫu lần lượt là 26 và 10
phân số có dạng \(\frac{26}{10}\) tối giản đi được \(\frac{13}{5}\)
đáp số là \(\frac{13}{5}\) nhá bạn, mình ko nhớ kiến thức cơ bản nên cũng phải học lại cái đó mới ra dc bài này, phân số thập phân học từ lp 5 rồi nhá

a) Ta có: \(N=\left(-\dfrac{3}{4}xy^4\right)\cdot\left(\dfrac{6}{9}x^2y^2\right)\)
\(=\left(-\dfrac{3}{4}\cdot\dfrac{6}{9}\right)\cdot\left(x\cdot x^2\right)\cdot\left(y^4\cdot y^2\right)\)
\(=-\dfrac{1}{2}x^3y^6\)
Hệ số: \(-\dfrac{1}{2}\)
Phần biến: \(x^3;y^6\)
Bậc của đơn thức là 9

a) Ta có:
\(P\left(x\right)=5x^3+2x^4-x^2+3x^2-3x^3-x^4+1-4x^3\)
\(\Rightarrow P\left(x\right)=2x^4-x^4+5x^3-3x^3-4x^3-x^2+3x^2+1\)
\(\Rightarrow P\left(x\right)=x^4-2x^3+2x^2+1\)

\(\left(-\dfrac{1}{3}3m^2\right).\left(-24n\right)nn.\left(4mn\right)\)
=\(\left(-\dfrac{1}{3}.\left(-24\right).4\right).\left(m^2.m\right).\left(n.n\right)\)
=32.m3.n2
phần hệ số : 32
Phần biến : m3.n2
bậc : 3+2=5

Bài làm:
Vì a,b,c khác 0 nên:
Ta có: \(a\left(y+z\right)=b\left(z+x\right)=c\left(x+y\right)\)
\(\Leftrightarrow\frac{y+z}{bc}=\frac{z+x}{ca}=\frac{x+y}{ab}\) (1) (chia cả 3 vế cho abc)
Áp dụng t/c dãy tỉ số bằng nhau ta được:
\(\left(1\right)=\frac{x+y-z-x}{ab-ca}=\frac{y+z-x-y}{bc-ab}=\frac{z+x-y-z}{ca-bc}\)
\(=\frac{y-z}{a\left(b-c\right)}=\frac{z-x}{b\left(c-a\right)}=\frac{x-y}{c\left(a-b\right)}\)
=> đpcm
Bài làm:
Vì a,b,c khác 0 nên:
Ta có: a(y+z)=b(z+x)=c(x+y)�(�+�)=�(�+�)=�(�+�)
⇔y+zbc=z+xca=x+yab⇔�+���=�+���=�+��� (1) (chia cả 3 vế cho abc)
Áp dụng t/c dãy tỉ số bằng nhau ta được:
(1)=x+y−z−xab−ca=y+z−x−ybc−ab=z+x−y−zca−bc(1)=�+�−�−���−��=�+�−�−���−��=�+�−�−���−��
=y−za(b−c)=z−xb(c−a)=x−yc(a−b)=�−��(�−�)=�−��(�−�)=�−��(�−�)
=> đpcm