
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(5n+2\right)^2-4=5n^2+2^2-4=5n^2⋮5\left(\text{đ}pcm\right)\)
Khai triển phương trình :
\(\left(5n+2\right)^2-4\)
\(=\left(25n^2+2.2.5n+2^2\right)-4\)
\(=25n^2+20n+4-4\)
\(=25n^2+20n\)
\(=5n\left(5n+4\right)\)
\(\Rightarrow\left(52+2\right)^2-4=5n\left(5n+4\right)⋮5\)

\(n\left(5n-1\right)-5n\left(n+2\right)=5n^2-n-5n^2-10n=-11n⋮11\forall n\in Z\)

Ta có:
\(n\left(5n-2\right)-5n\left(n+3\right)\)
\(=n\left(5n-2\right)-n\left(5n+3\right)\)|
\(=n\left(5n-2-5n-3\right)=-5n\) ; Vì \(n\in Z\)
\(\Rightarrow-5n\in Z\Rightarrow
-5n⋮-5\)
Vậy: .......
#HọcTốt!!

bài này dễ mà. như sau nhé :
(5n+2)2-4= 25n2+20n+4-4 (áp dụng hằng đẳng thức số 1)
= 25n2+20n
Vì 25 chia hết cho 5 => 25n2 chia hết cho 5 với mọi số nguyên n
20 chia hết cho 5 => 20n chia hết cho 5 với mọi số nguyên n
=> (25n2 + 20n) chia hết cho 5 với mọi số nguyên n
=> (5n +2)2 - 4 chia hết cho 5 với mọi số nguyên n
k cko mk nhé !!!
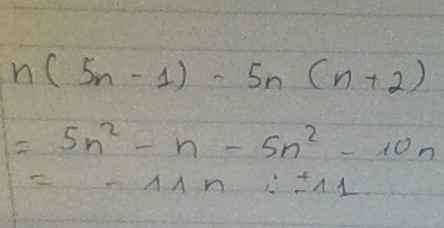
=25n2+20n