
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2:
a) ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\notin\left\{4;9\right\}\end{matrix}\right.\)
b) Ta có: \(B=\dfrac{2\sqrt{x}-9}{x-5\sqrt{x}+6}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}-\dfrac{2\sqrt{x}+1}{3-\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}-9-\left(x-9\right)+\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{2\sqrt{x}-9-x+9+2x-4\sqrt{x}+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\cdot\left(\sqrt{x}-3\right)}\)
\(=\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)
c) Để B>1 thì B-1>0
\(\Leftrightarrow\dfrac{\sqrt{x}+1}{\sqrt{x}-3}-\dfrac{\sqrt{x}-3}{\sqrt{x}-3}>0\)
\(\Leftrightarrow\dfrac{4}{\sqrt{x}-3}>0\)
\(\Leftrightarrow\sqrt{x}>3\)
hay x>9
Bài 2:
d) Để B nguyên thì \(\sqrt{x}+1⋮\sqrt{x}-3\)
\(\Leftrightarrow4⋮\sqrt{x}-3\)
\(\Leftrightarrow\sqrt{x}-3\in\left\{-2;-1;1;2;4\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{1;2;4;5;7\right\}\)
hay \(x\in\left\{1;16;25;49\right\}\)


Đây nè :
y=x^3+3x^2+1=(x+1)^3-3x <=>
y-3=(x+1)^3-3x-3 hay
y-3 = (x+1)^3 - 3(x+1) (*)
Nhìn vào (*) ta thấy rằng nếu chọn hệ trục tọa độ mới IXY với gốc tọa độ tại I(-1;3)
Khi đó X=x+1, Y=y-3 và hàm số trở thành Y=X^3 - 3X là hàm lẻ, đồ thị của nó (cũng chính là đồ thị hàm đã cho trong hệ tọa độ cũ) nhận I là tâm đối xứng.
Vậy tâm đối xứng của đồ thị hs đã cho là I(-1;3)
Nếu bạn đã học khảo sát hàm số bằng đạo hàm thì có cách này đơn giản hơn nhiều :
y'=3x^2+6x (nghiệm của y'=0 là hoành độ các cực trị, nhưng ta không quan tâm)
y''=6x+6 (nghiệm của y''=0 chính là hoành độ điểm uốn, cũng là tâm đối xứng)
y''=6x+6=0=>x= -1=>y=3

\(a\left(a+2\right)< \left(a+1\right)^2\)
\(\Leftrightarrow a^2+2a< a^2+2a+1\)
\(\Leftrightarrow0< 1\)(luôn đúng)
Do bđt cuối luôn đúng nên bđt ban đầu đc cm
Do a2 + 2a < a2 + 2a + 1
=> a.(a + 2) < a2 + a + a + 1
=> a.(a + 2) < a.(a + 1) + (a + 1)
=> a.(a + 2) < (a + 1)2 (đpcm)

Bài 1:
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=3.6\left(cm\right)\\CH=6.4\left(cm\right)\end{matrix}\right.\)
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HF là đường cao ứng với cạnh huyền AB, ta được:
\(AF\cdot AB=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:
\(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AF\cdot AB=AE\cdot AC\)

Gọi số ngày hoàn thành công việc nếu làm riêng của người thứ nhất là x, người thứ 2 là y(ngày),(x,y>0)
1 ngày người thứ nhất làm được:\(\frac{1}{x}\)
1 ngày người thứ hai làm được:\(\frac{1}{y}\)
=> 1 ngày cả người làm được:\(\frac{1}{x}+\frac{1}{y}=\frac{1}{12}\)(1)
3 ngày người thứ nhất làm được:\(\frac{3}{x}\)
Vì sau 3 ngày, người thứ 2 làm nốt 15 ngày nên: Số ngày người thứ 2 làm là 15+3=18
18 ngày người thứ hai làm được \(\frac{18}{x}\)
Do đó, ta được:\(\frac{3}{x}+\frac{18}{y}=1\)(2)
Từ (1) và (2) , ta có hệ: \(\hept{\begin{cases}\frac{1}{x}+\frac{1}{y}=\frac{1}{12}\\\frac{3}{x}+\frac{18}{y}=1\end{cases}}\)
Đặt \(\frac{1}{x}\)= a, \(\frac{1}{y}\)= b, ta được
\(\hept{\begin{cases}a+b=\frac{1}{12}\\3a+18b=1\end{cases}}\)<=>\(\hept{\begin{cases}a=\frac{1}{30}\\b=\frac{1}{20}\end{cases}}\)<=>\(\hept{\begin{cases}x=30\\y=20\end{cases}}\). Vậy......


a) Xét pt hoành độ gđ của (P) và (d) có:
\(\dfrac{1}{2}x^2=mx+2\) \(\Leftrightarrow x^2-2mx-4=0\) (1)
Có \(ac=1.\left(-4\right)< 0\)
=>Pt (1) luôn có hai nghiệm trái dấu
=> (P) và (d) luôn cắt nhau tại hai điểm phân biệt
b) \(M=\left(d\right)\cap Oy\Rightarrow M\left(0;2\right)\) \(\Rightarrow OM=2\)
Nhận xét: (P) luôn nằm phia trên trục hoành
(d) luôn cắt (P) tại hai điểm A(x1;y1) và B(x2;y2) với x1;x2 là hai nghiệm của pt (1) , x1.x2<0
=> A;B nằm khác phía nhau so với trục tung
Theo viet: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=-4\end{matrix}\right.\)
Do H và K lần lượt là hình chiếu của A và B trên trục hoành
=> \(OH=\left|x_1\right|\), \(OK=\left|x_2\right|\)
\(S_{MHK}=\dfrac{1}{2}.MO.HK=\dfrac{1}{2}.2\left(\left|x_1\right|+\left|x_2\right|\right)\)
\(\Leftrightarrow4=\left|x_1\right|+\left|x_2\right|\) \(\Leftrightarrow16=x_1^2+x_2^2+2\left|x_1x_2\right|\)
\(\Leftrightarrow16=\left(x_1+x_2\right)^2-2x_1x_2-2x_1x_2\) (do x1x2<0 => |x1x2|=-x1x2)
\(\Leftrightarrow16=4m^2-2\left(-4\right)-2\left(-4\right)\)
\(\Leftrightarrow m=0\)
Vậy...

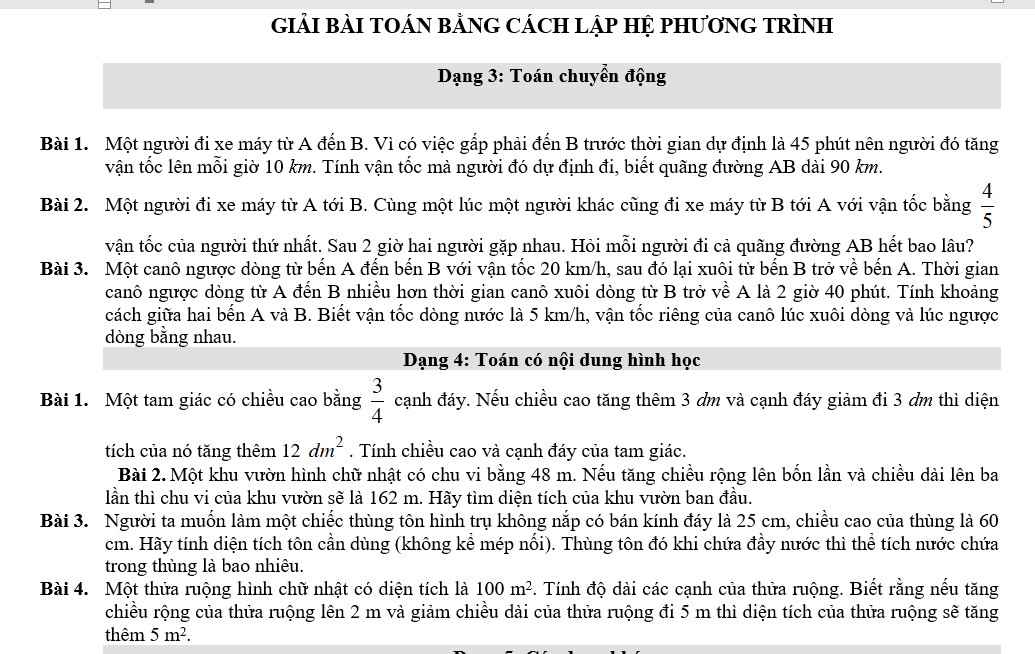


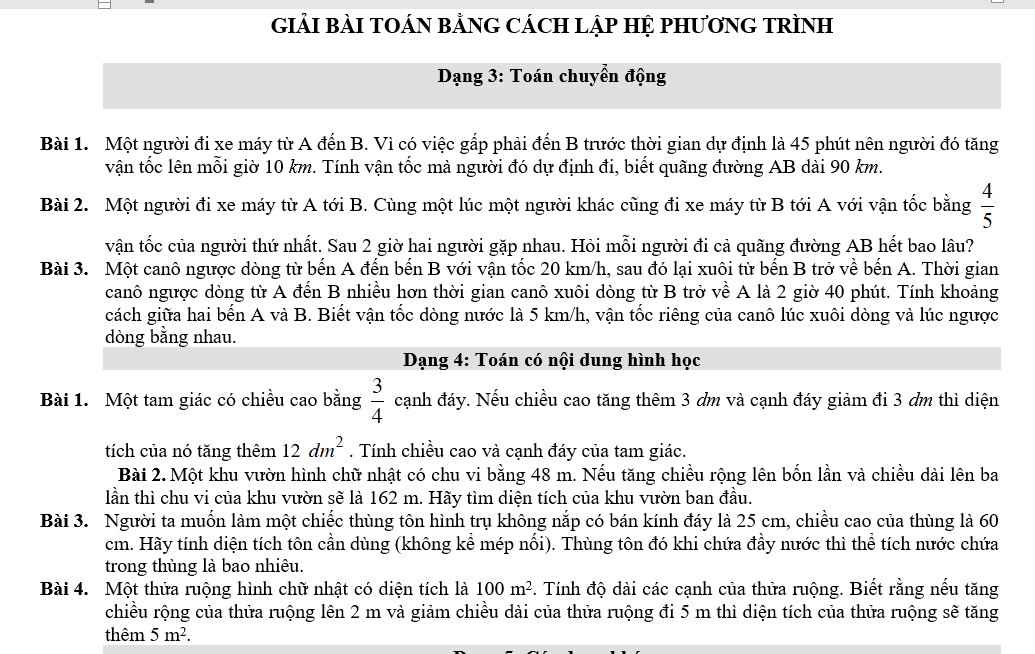 các bạn giúp mình với mình đang cần gấp
các bạn giúp mình với mình đang cần gấp 
mình chỉ gợi ý phương pháp giải thôi nha. Mình làm cho thì bạn hơi thụ động
Bài 8
1. chia cả tử và mẫu cho cosa. góc a nhọn thì bạn sẽ lựa góc phần tư
2. chia cả tử và mẫu cho cos^3 a. sử dụng các công thức lượng giác để đưa về cùng 1 đại lượng. góc a nhọn thì bạn sẽ lựa góc phần tư.
Bài 9
a) 1-(cos^2)a= -cos2a
b) 1 +(sin^2)a+(cos^2)a=2
c) sina(1-cos^2a)=sin^3a
bài 10:
sin^2a+cos^2a=1
=> cos^2=16/25
Vì a nhọn nên cosa dương => cos a=4/5
tana=3/4, cota= 4/3
2) có 1+tan^2x=1/cos^2x
=> cos^2x=1225/1369
x nhọn và tanx >0 nên sin>0 cos>0
=> cosx=35/37
=> sinx = 12/37
3) góc alpha nhọn => sina >0
-> sina = 12/13
tana = 12/5, cota= 5/12