
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Theo bài ra, ta có: a+b+c
Suy ra: 3(a+b+c)-3abc=0
Suy ra: -3abc=0
Tương đương: -3*(b+c)*(a+c)*(a+b)=0
Tương đương: -3* a^2+b^2+c^2=0
Tương đương: -3*0=0
Suy ra: nếu a+b+c=0 thì a3+b3+c3-3abc=0(đpcm)


Từ đẳng thức đã cho suy ra a 3 + b 3 + c 3 – 3abc = 0
b 3 + c 3 = (b + c)( b 2 + c 2 – bc)
= (b + c)[ ( b + c ) 2 – 3bc]
= ( b + c ) 3 – 3bc(b + c)
=> a 3 + b 3 + c 3 – 3abc = a 3 + ( b 3 + c 3 ) – 3abc
ó a 3 + b 3 + c 3 – 3abc = a 3 + ( b + c ) 3 – 3bc(b + c) – 3abc
ó a 3 + ( b 3 + c 3 ) – 3abc = (a + b + c)( a 2 – a ( b + c ) + ( b + c ) 2 ) – [3bc(b + c) + 3abc]
ó a 3 + ( b 3 + c 3 ) – 3abc = (a + b + c)( a 2 – a ( b + c ) + ( b + c ) 2 ) – 3bc(a + b + c)
ó a 3 + ( b 3 + c 3 ) – 3abc = (a + b + c)( a 2 – a ( b + c ) + ( b + c ) 2 – 3bc)
ó a 3 + ( b 3 + c 3 ) – 3abc = (a + b + c)( a 2 – ab - ac + b 2 + 2bc + c 2 – 3bc)
ó a 3 + ( b 3 + c 3 ) – 3abc = (a + b + c)( a 2 + b 2 + c 2 – ab – ac – bc)
Do đó nếu a 3 + ( b 3 + c 3 ) – 3abc = 0 thì a + b + c = 0 hoặc a 2 + b 2 + c 2 – ab – ac – bc = 0
Mà a 2 + b 2 + c 2 – ab – ac – bc = .[ ( a – b ) 2 + ( a – c ) 2 + ( b – c ) 2 ]
Nếu ( a – b ) 2 + ( a – c ) 2 + ( b – c ) 2 = 0 ó suy ra a = b = c
Vậy a 3 + ( b 3 + c 3 ) = 3abc thì a = b = c hoặc a + b + c = 0
Đáp án cần chọn là: C

Bài 1:
$a^3+b^3+c^3=3abc$
$\Leftrightarrow (a+b)^3-3ab(a+b)+c^3-3abc=0$
$\Leftrightarrow [(a+b)^3+c^3]-[3ab(a+b)+3abc]=0$
$\Leftrightarrow (a+b+c)[(a+b)^2-c(a+b)+c^2]-3ab(a+b+c)=0$
$\Leftrightarrow (a+b+c)[(a+b)^2-c(a+b)+c^2-3ab]=0$
$\Leftrightarrow (a+b+c)(a^2+b^2+c^2-ab-bc-ac)=0$
$\Rightarrow a+b+c=0$ hoặc $a^2+b^2+c^2-ab-bc-ac=0$
Xét TH $a^2+b^2+c^2-ab-bc-ac=0$
$\Leftrightarrow 2(a^2+b^2+c^2)-2(ab+bc+ac)=0$
$\Leftrightarrow (a-b)^2+(b-c)^2+(c-a)^2=0$
$\Rightarrow a-b=b-c=c-a=0$
$\Leftrightarrow a=b=c$
Vậy $a^3+b^3+c^3=3abc$ khi $a+b+c=0$ hoặc $a=b=c$
Áp dụng vào bài:
Nếu $a+b+c=0$
$A=\frac{-c}{c}+\frac{-b}{b}+\frac{-a}{a}=-1+(-1)+(-1)=-3$
Nếu $a=b=c$
$P=\frac{a+a}{a}+\frac{b+b}{b}+\frac{c+c}{c}=2+2+2=6$

có:a+b+c=0 suy ra :a+b= -c(1)
(a+b)^3= -c^3
a^3+3a^2b+3ab^2+3b^3+c^3=0
a^3+b^3+c^3+3ab(a+b)=0
a^3+b^3+c^3-3abc=0(Vì a+b= -c)
a^3+b^3+c^3 =3abc

a) Áp dụng nhiều lần công thức \(\left(x+y\right)^3=x^3-y^3+3xy\left(x+y\right)\), ta có:
\(\left(a+b+c\right)^3-a^3-b^3-c^3\)
\(=\left[\left(a+b\right)+c\right]^3-a^3-b^3-c^3\)
\(=\left(a+b\right)^3+c^3+3c\left(a+b\right)\left(a+b+c\right)-a^3-b^3-c^3\)
\(=a^3+b^3+3ab\left(a+b\right)+c^3+3c\left(a+b\right)\left(a+b+c\right)-a^3-b^3-c^3\)
\(=3\left(a+b\right)\left(ab+ac+bc+c^2\right)\)
\(=3\left(a+b\right)\left[a\left(b+c\right)+c\left(b+c\right)\right]\)
\(=3\left(a+b\right)\left(b+c\right)\left(a+c\right)\left(Đpcm\right)\)
b) Ta có:
\(a^3+b^3+c^3-3abc\)
\(=a^3+3ab\left(a+b\right)+b^2+c^3-3abc-3ab\left(a+b\right)\)
\(=\left(a+b\right)^3+c^3-3ab\left(a+b+c\right)\)
\(=\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2\right)-3ab\left(a+b+c\right)\)
\(=\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2-3ab\right)\)
\(=\left(a+b+c\right)\left(a^2+b^2+c^2-ac-bc-ab\right)\)
Mình nghĩ bằng thế này mới đúng, bạn chắc ghi sai đề rồi ![]()
a) Ta có: (a + b + c)3 - a3 - b3 - c3 = [ (a + b + c)3 - a3 ] - ( b3 + c3)
= (a + b + c - a) ( a2 + b2 + c2 + 2ab + 2bc + 2ac + a2 + ab + ac + a2) - (b + c) ( b2 - bc + c3)
= (b + c) ( 3a2 + b2 + c2 + 3ab + 2bc + 3ac) - (b + c) ( b2 - bc + c3)
= ( b + c) ( 3a2 + b2 + c2 + 3ab + 2bc + 3ac - b2 + bc - c3)
= ( b + c) ( 3a2 + 3ab + 3bc + 3ac)
= 3 (b + c) [a (a + b) + c (a + b)]
= 3 (b + c) (a + b) (a + c) (đpcm)

Từ đẳng thức đã cho suy nghĩ a 3 + b 3 + c 3 – 3abc = 0
B 3 + c 3 = ( b + c ) ( b 2 + c 2 – b c ) = ( b + c ) [ ( b + c ) 2 – 3 b c ] 4 = ( b + c ) 3 – 3 b c ( b + c )
= > a 3 + b 3 + c 3 – 3 a b c = a 3 + ( b 3 + c 3 ) – 3 a b c ⇔ a 3 + b 3 + c 3 – 3 a b c = a 3 + ( b 3 + c 3 ) – 3 b c ( b + c ) – 3 a b c ⇔ a 3 + b 3 + c 3 – 3 a b c = ( a + b + c ) ( a 2 – a ( b + c ) + ( b + c ) 2 ) – [ 3 b c ( b + c ) + 3 a b c ] ⇔ a 3 + b 3 + c 3 – 3 a b c = ( a + b + c ) ( a 2 – a ( b + c ) + ( b + c ) 2 ) – 3 b c ) ⇔ a 3 + b 3 + c 3 – 3 a b c = ( a + b + c ) ( a 2 – a b – a c + b 2 + 2 b c + c 2 – 3 b c ) ⇔ a 3 + b 3 + c 3 – 3 a b c = ( a + b + c ) ( a 2 + b 2 + c 2 – a b – a c – b c )
Do đó nếu a 3 + b 3 + c 3 – 3abc = 0 thì a + b + c = 0 hoặc a 2 + b 2 + c 2 – ab – ac – bc = 0
Mà a 2 + b 2 + c 2 – ab – ac – bc = .[ ( a – b ) 2 + ( a – c ) 2 + ( b – c ) 2 ]
Suy ra a = b = c
Đáp án cần chọn là: B

Câu hỏi của trần thị bảo trân - Toán lớp 8 - Học toán với OnlineMath
Tham khảo ở link trên nhé.
\(a+b+c=0\)
\(-a=b+c\)
\(\Rightarrow-a^3=\left(b+c\right)^3\)
\(\Rightarrow-a^3=b^3+c^3+3bc\left(b+c\right)\)
\(\Rightarrow a^3+b^3+c^3=3abc\)
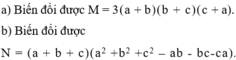
(a+b+c)(a2+b2+c2−ab−ac−bc)(a+b+c)(a2+b2+c2−ab−ac−bc)
cái này cần thêm 1 chút chi tiết nữa mới tuột :D