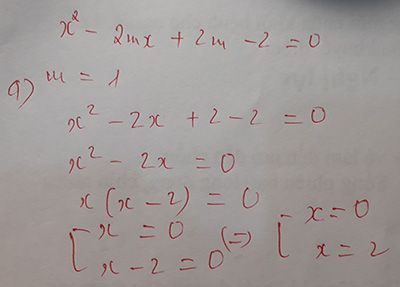Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c) tim x1 và x2 theo ct;
x1= 16 +can denta ....tu lam
d) c/a <0
lam dc roi chu

câu a bạn áp dụng hệ thức Viet rồi rút m và thay vào cái kia r tìm ra thôi
![]()

Theo định lý Vi-ét có :
\(\hept{\begin{cases}x_1+x_2=-m\\x_1x_2=-35\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x_1+x_2=-m\\7\cdot x_2=-35\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x_1+x_2=-m\\x_2=-5\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}m=-\left(7-5\right)=-2\\x_2=-5\end{cases}}\)
P/s : E mới đọc cái định lý này, sai ở đâu thì mọi người cho e ý kiến với ạ :)) E cảm ơn !!

\(a,\Delta=m^2-4m+4=\left(m-2\right)^2\ge0\forall m\)
Nên pt đã cho luôn có 2 nghiệm phân biệt với mọi m
b, Theo Vi-ét \(\hept{\begin{cases}x_1+x_2=m\\x_1x_2=m-1\end{cases}}\)
Ta có \(B=\frac{2x_1x_2+3}{x_1^2+x_2^2+2\left(1+x_1x_2\right)}=1\)
\(\Leftrightarrow\frac{2x_1x_2+3}{\left(x_1+x_2\right)^2+2}=1\)
\(\Leftrightarrow\frac{2\left(m-1\right)+3}{m^2+2}=1\)
\(\Leftrightarrow\frac{2m+1}{m^2+2}=1\)
\(\Leftrightarrow2m+1=m^2+2\)
\(\Leftrightarrow m^2-2m+1=0\)
\(\Leftrightarrow\left(m-1\right)^2=0\)
\(\Leftrightarrow m=1\)

\(x^2-2mx+m-7=0\)
Phương trình đã cho luôn có 2 nghiệm pb
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=m-7\end{matrix}\right.\)
a/ \(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=2m\\2x_1x_2=2m-14\end{matrix}\right.\)
Trừ vế cho vế: \(x_1+x_2-2x_1x_2=14\)
Đây là hệ thức liên hệ 2 nghiệm ko phụ thuộc m
\(\Rightarrow x_1\left(1-2x_2\right)=14-x_2\)
\(\Rightarrow x_1=\frac{14-x_2}{1-2x_2}\)
b/ \(\frac{1}{x_1^3}+\frac{1}{x_2^3}=\frac{x_1^3+x_2^3}{\left(x_1x_2\right)^3}=\frac{\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)}{\left(x_1x_2\right)^3}=\frac{8m^3-6m\left(m-7\right)}{\left(m-7\right)^3}\)
\(A=2\left(x_1^2+x_2^2\right)+x_1^2-2mx_1+m\)
Mặt khác do \(x_1\) là nghiệm nên
\(x_1^2-2mx_1+m=7\)
\(\Rightarrow A=2\left(x_1^2+x_2^2\right)+7=2\left(x_1+x_2\right)^2-4x_1x_2+7\)
\(=8m^2-4\left(m-7\right)+7=8m^2-4m+35\)
c/ Để pt có 2 nghiệm dương:
\(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2>0\\x_1x_2>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2m>0\\m-7>0\end{matrix}\right.\) \(\Rightarrow m>7\)