Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\sin\alpha=\frac{2}{5}\)
\(\Rightarrow\cos\alpha=\sqrt{1-\sin^2\alpha}\)
\(=\sqrt{1-\frac{4}{25}}\)
\(=\sqrt{\frac{21}{25}}=\)\(\frac{\sqrt{21}}{5}\)
\(\Rightarrow\tan\alpha=\frac{\sin\alpha}{\cos\alpha}=\frac{2}{5}:\frac{\sqrt{21}}{5}=\frac{2}{\sqrt{21}}\)và \(\cot\alpha=\frac{\sqrt{21}}{2}\)
2. Tương tự a)
\(\cos B=\sqrt{1-\sin^2B}\)
\(=\sqrt{1-\frac{1}{4}}\)
\(=\sqrt{\frac{3}{4}}=\frac{\sqrt{3}}{2}\)
\(\tan B,\cot B\)bạn tự tính nốt.
\(sin\alpha=0,4\Rightarrow sin^2\alpha=0,16\Rightarrow cos^2\alpha=1-sin^2\alpha=1-0,16=0,84\Rightarrow cos\alpha=\frac{\sqrt{21}}{5}\)
\(tan\alpha=\frac{sin\alpha}{cos\alpha}=\frac{0,4}{\frac{\sqrt{21}}{5}}=\frac{2\sqrt{21}}{21}\)
\(cot\alpha=1:sin\alpha=1:\frac{2\sqrt{21}}{21}=\frac{21}{2\sqrt{21}}\)

Ta có CT: sin^2a+cos^2a=1 => cos^2a=1-sin^2a=0,64 => cosa=0,8
Áp dụng 2 công thức sau và làm tương tự:
tana=sina/cosa
cota=cosa/sina

ta co \(sin^2a+cos^2a=1\Rightarrow cosa=0.36\)
\(\frac{sina}{cosa}=tana\Rightarrow tana=\frac{20}{9}\)
\(tana\cdot cotga=1\Rightarrow cotga=\frac{9}{20}\)
câu b tương tự nha cau c \(\frac{sina+cosa}{sina-cosa}=\) bn

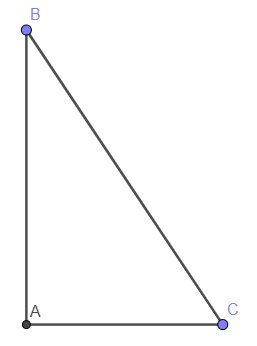
Xét \(\Delta ABC\) vuông tại A có:
\(sin\left(B\right)=\dfrac{AC}{BC}\)
\(cotg\left(C\right)=\dfrac{AC}{AB}\)
BC là cạnh huyền của \(\Delta ABC\) \(\left(AB,AC< BC\right)\)
\(\Rightarrow\dfrac{AC}{BC}< \dfrac{AC}{AB}\Rightarrow sin\left(B\right)< cotg\left(C\right)\)

căn(x^2- 2.3.x + 3^2) +căn (x^2+ 2.5.x +5^2) =8
tđ căn( x-3)^2 + căn (x+5)^2 =8
tđ /x-3/ + /x+5/ =8
tđ x - 3 + x + 5 =8
tđ 2x - 2 = 8
tđ 2( x - 1) =8
tđ x-1 =4
tđ x =5
NGUYỄN HƯƠNG GIANG,chào bạn,cảm ơn bạn đã quan tâm đến câu hỏi của mình,nhưng mik không hiểu cách bạn làm ạ,ở đây không hề cho điều kiện x,cho nên việc bạn bỏ dấu trị tuyệt đối như vậy có đúng không ạ?giải thích giúp mik nhé,cảm ơn bạn
tỉ số lượng giác ( sin , cos , tan , cot ) chỉ áp dụng được trong tam giác vuông thôi bạn ạ
Ok cảm ơn bạn thanks bạn nhiều nha