Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) 3x2y3+x2y3=4x2y3
b)5x2y-1/2x2y=10/2x2y-1/2x2y=9/2x2y
c) \(\frac{3}{4}xyz^2+\frac{1}{2}xyz^2-\frac{1}{4}xyz^2\)
\(=\frac{3}{4}xyz^2+\frac{2}{4}xyz^2-\frac{1}{4}xyz^2\)
\(=\frac{5}{4}xyz^2-\frac{1}{4}xyz^2\)
\(=\frac{4}{4}xyz^2=xyz^2\)
\(a,3x^2y^3+x^2y^3=4x^2y^3\)
\(b,5x^2y-\frac{1}{2}x^2y=\frac{9}{2}x^2y\)
\(c,\frac{3}{4}xyz^2+\frac{1}{2}xyz^2-\frac{1}{4}xyz^2=\left(\frac{3}{4}xyz^2-\frac{1}{4}xyz^2\right)+\frac{1}{2}xyz^2=\frac{2}{4}xyz^2+\frac{1}{2}xyz^2=xyz^2\)

\(\left(x^2-1\right).\left(x^2-9\right)\)
\(=x^4-9x^2-x^2+9\)
\(=x^4-10x^2+9\)
\(=\left(x^2\right)^2-2.x^2.5+25-16\)
\(=\left(x^2-5\right)^2-16\ge-16\)
=> GTNN của B.thức trên là -16
<=> \(x^2-5=0\Leftrightarrow x^2=5\Leftrightarrow x=\sqrt{5}\text{ hoặc }x=-\sqrt{5}\)
Vậy...

Giải
Kiểm tra:

Ta có thể viết được các tỉ số khác nhau cũng có thể "rút gọn" như vậy
Chẳng hạn:
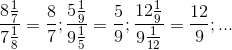

Gọi kết quả thứ 1 là b, số hữu tỉ cần tìm là a
Ta có:
\(a+3\frac{5}{7}=b\)
\(b-\frac{22}{5}=5,75\)\(\Rightarrow b=5.57+\frac{22}{5}=9.97\)
\(\Rightarrow a+3\frac{5}{7}=9,97\)\(\Rightarrow a=9,97-3\frac{5}{7}=\frac{4379}{700}=6,25\left(571428\right)\)
Vậy số hữu tỉ là \(6,25\left(571428\right)\)