PC
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
4 tháng 2 2019
\(C=\frac{x+5}{2x+\left(x-2y\right)}+\frac{y-5}{2y-\left(x-2y\right)}\)
\(=\frac{x+5}{2x+10}+\frac{y-5}{2y-10}=\frac{x+5}{2\left(x+5\right)}+\frac{y-5}{2\left(y-5\right)}=\frac{1}{2}+\frac{1}{2}=1\left(x\ne-5,y\ne5\right)\)
BN
4 tháng 2 2019
Trả lời :
Ta có :
C = \(\frac{x+5}{3x-2y}+\frac{y-5}{4y-x}\)
C = \(\frac{2\left(x+5\right)}{2\left(3x-2y\right)}+\frac{2\left(y-5\right)}{2\left(4y-x\right)}\)
C = \(\frac{2x+10}{6x-4y}+\frac{2y-10}{8y-2x}\)
Thay x - 2y = 10 . Ta được :
C = \(\frac{2x+x-2y}{6x-4y}+\frac{2y-x-2y}{8y-2x}\)
C = \(\frac{x\left(2+1\right)-2y}{6x-4y}+\frac{y\left(2+2\right)-x}{8y-2x}\)
C = \(\frac{3x-2y}{6x-4y}+\frac{4y-x}{8y-2x}\)
C = \(\frac{1}{2}+\frac{1}{2}\)
C = \(1\)
Vậy C = 1
Hok tốt
25 tháng 6 2022
a: \(3x^2\left(2x^3-x+5\right)\)
\(=3x^2\cdot2x^3-3x^2\cdot x+5\cdot3x^2\)
\(=6x^5-3x^3+15x^2\)
b: \(x^2y\left(4xy+3y-5x\right)\)
\(=x^2y\cdot4xy+x^2y\cdot3y-x^2y\cdot5x\)
\(=4x^3y^2+3x^2y^2-5x^3y\)
XO
23 tháng 9 2020
Ta có :\(15x=10y=6z\Rightarrow\hept{\begin{cases}15x=10y\\10y=6z\end{cases}}\Rightarrow\hept{\begin{cases}3x=2y\\5y=3z\end{cases}}\Rightarrow\hept{\begin{cases}\frac{x}{2}=\frac{y}{3}\\\frac{y}{3}=\frac{z}{5}\end{cases}}\Rightarrow\frac{x}{2}=\frac{y}{3}=\frac{z}{5}\)
Đặt \(\frac{x}{2}=\frac{y}{3}=\frac{z}{5}=k\Rightarrow\hept{\begin{cases}x=2k\\y=3k\\z=5k\end{cases}}\)
Khi đó 5x3 + 2y3 - z3 = 31
=> 5(2k)3 + 2(3k)3 - (5k)3 = 31
=> 40k3 + 54k3 - 125k3 = 31
=> -31k3 = 31
=> k3 = -1
=> k = -1
=> x = -2 ; y = -3 ; z = -5
b) Ta có 7x = 14y = 6z => \(\hept{\begin{cases}7x=14y\\14y=6z\end{cases}}\Rightarrow\hept{\begin{cases}x=2y\\7y=3z\end{cases}}\Rightarrow\hept{\begin{cases}\frac{x}{2}=\frac{y}{1}\\\frac{y}{3}=\frac{z}{7}\end{cases}}\Rightarrow\hept{\begin{cases}\frac{x}{6}=\frac{y}{3}\\\frac{y}{3}=\frac{z}{7}\end{cases}}\Rightarrow\frac{x}{6}=\frac{y}{3}=\frac{z}{7}\)
Đặt \(\frac{x}{6}=\frac{y}{3}=\frac{z}{7}=k\Rightarrow\hept{\begin{cases}x=6k\\y=3k\\z=7k\end{cases}}\)
Khi đó 2x2 - 3y2 = 5
<=> 2.(6k)2 - 3.(3k)2 = 5
=> 72k2 - 27k2 = 5
=> 45k2 = 5
=> k2 = 1/9
=> k = \(\pm\frac{1}{3}\)
Nếu k = 1/3 => x = 2 ; y = 1 ; z = 7/3
Nếu k = -1/3 => x = -2 ; y = - 1 ; z = -7/3
Vậy các cặp (x;y;z) thỏa mãn là : (2;1;7/3) ; (-2 ; - 1; -7/3)
c) Ta có : \(3x=8y=5z\Rightarrow\frac{3x}{120}=\frac{8y}{120}=\frac{5z}{120}\Rightarrow\frac{x}{40}=\frac{y}{15}=\frac{z}{24}\)
Đặt \(\frac{x}{40}=\frac{y}{15}=\frac{z}{24}=k\Rightarrow\hept{\begin{cases}x=40k\\y=15k\\z=24k\end{cases}}\)
Khi đó |x - 2y| = 5
<=> |40k - 2.15k| = 5
=> |10k| = 5
=> \(\orbr{\begin{cases}10k=5\\10k=-5\end{cases}}\Rightarrow\orbr{\begin{cases}k=\frac{1}{2}\\k=-\frac{1}{2}\end{cases}}\)
Nếu k = 5 => x = 20 ; y = 7,5 ; z = 12
Nếu k = -5 => x = -20 ; y =-7,5 ; z = -12
d) 4x = 5y = 6z => \(\frac{4x}{60}=\frac{5y}{60}=\frac{6z}{60}\Rightarrow\frac{x}{15}=\frac{y}{12}=\frac{z}{10}\)
Đặt \(\frac{x}{15}=\frac{y}{12}=\frac{z}{10}=k\Rightarrow\hept{\begin{cases}x=15k\\y=12k\\z=10k\end{cases}}\)
Khi đó (3x - 2y)2 = 16
<=> (3.15k - 2.12k)2 = 16
=> (45k -24k)2 = 16
=> (21k)2 = 16
=> \(\orbr{\begin{cases}21k=4\\21k=-4\end{cases}}\Rightarrow\orbr{\begin{cases}k=\frac{4}{21}\\k=-\frac{4}{21}\end{cases}}\)
Nếu k = 4/21 => x = 20/7 ; y = 16/7 ; z = 40/21
Nếu k = -4/21 => x = -20/7 ; y = -16/7 ; z = -40/21
29 tháng 7 2023
P(x)+Q(x)
=3x^2y-2x+5xy^2-7y^2+3xy^2-7y^2-9x^2y-x-5
=8xy^2-14y^2-6x^2y-3x-5
=>Chọn A
12 tháng 3 2018
BÀI 1:
A) THAY X =2 ; Y= 1/3 VÀO BIỂU THỨC
2. ( 2+ 2) + 1/3. ( 1/3 + 3) + 2^2 + 2. (1/3) ^2 + 4. 1/3
= 2.4 + 1/3 . 10/3+ 4+ 2. 1/9 + 4/3
= 8+ 10/9 + 4+ 2/9 + 4/3
= 44/3
B) THAY X= 2; Y= 1/3 VÀO BIỂU THỨC
( 2 + 1/3 ) . 2 + ( 2- 1/3 ) . 2
= 7/3 . 2 + 5/3 . 2
= 7/6 + 10/3
= 9/2
C) TA CÓ: ( X+ Y) X + ( X+Y ) X= 2. X.( X+Y)
THAY X= 2; Y= 1/3 VÀO BIỂU THỨC
2. 2.( 2+ 1/3)
= 4. 7/3
= 28/3
BÀI 2:
A) \(\left(x^2+6x+5\right)+\left(-3x+9\right)=x^2+6x+5-3x+9\)
\(=\left(6x-3x\right)+\left(5+9\right)+x^2\)
\(=3x+14+x^2\)
B) \(\left(2x^2+3x+7\right)-\left(-2x+5\right)=2x^2+3x+7+2x-5\)
\(=2x^2+\left(3x+2x\right)+\left(7-5\right)\)
\(=2x^2+5x+2\)
C) \(\left(6x^2y-6xy^2\right)+\left(7xy+4xy^2-x^2y\right)=6x^2y-6xy^2+7xy+4xy^2-x^2y\)
\(=\left(6x^2y-x^2y\right)+\left(4xy^2-6xy^2\right)+7xy\)
\(=5x^2y+\left(-2xy^2\right)+7xy\)
CHÚC BN HỌC TỐT!!!!
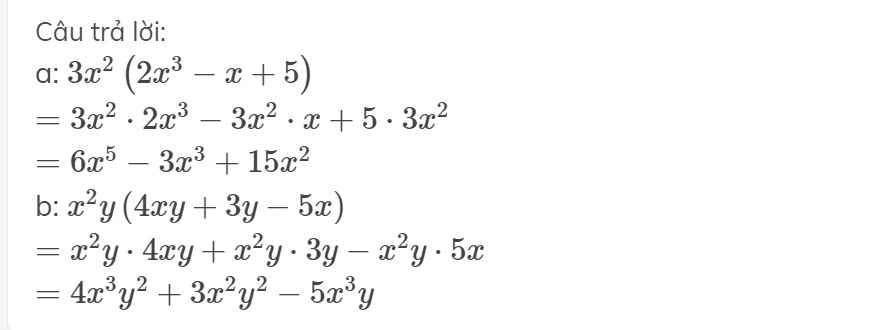
Ta thấy: \(\hept{\begin{cases}\left|3x+5\right|\ge0\\\left|2y-3\right|\ge0\end{cases}\forall x,y}\)
=> |3x + 5| + |2y - 3| \(\ge\)0
=> C = 5 + |3x + 5| + |2y - 3| \(\ge\)5
Dấu "=" xảy ra <=> \(\hept{\begin{cases}\left|3x+5\right|=0\\\left|2y-3\right|=0\end{cases}}\Rightarrow\hept{\begin{cases}x=\frac{-5}{3}\\y=\frac{3}{2}\end{cases}}\)
Vậy CMin = 5 tại x = -5/3 và y = 3/2