Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

* Số phần tử của không gian mẫu: Ω = C 100 5 .
* Trong 100 sản phẩm đó có 8 sản phẩm hỏng và 92 sản phẩm không hỏng nên số phần tử của biến cố A là: n A = C 8 2 . C 92 3 .
Xác suất của biến cố A : P A = n A Ω = 299 6402 .
Chọn đáp án B.

Chọn C
Số phần tử của không gian mẫu là: ![]() .
.
Gọi biến cố A: “ Hai người được chọn đều là nam”.
![]()
Vậy xác suất cần tìm là: 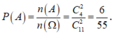 .
.

Bài giải
Gọi hệ trục Oxyz với A(0;0;0), B(a;0;0), C(a;a;0), D(0;a;0). Gọi S(p;q;h).
SA = SB = a:
p² + q² + h² = a²
(p - a)² + q² + h² = a² ⇒ p = a/2
SC = a√3:
a²/4 + (q - a)² + h² = 3a²
Từ SA: q² + h² = 3a²/4 ⇒ a²/4 + q² - 2aq + a² + h² = 3a²
2a² - 2aq = 3a² ⇒ q = -a/2 ⇒ h² = a²/2 ⇒ h = a√2/2
S(a/2; -a/2; a√2/2)
H(a/4; -a/4; a√2/4), K(3a/4; -a/4; a√2/4)
M(x; x; 0), 0 ≤ x ≤ a
N(a; t; 0) ∈ BC
HK = (a/2; 0; 0)
HM = (x - a/4; x + a/4; -a√2/4)
n = HK × HM = (0; a²√2/8; a/2(x + a/4))
Mặt phẳng (HKM): (a²√2/8)(y + a/4) + (a/2)(x + a/4)(z - a√2/4) = 0
Với N(a; t; 0): t = x ⇒ N(a; x; 0)
HK = a/2, MN = a - x
d = √[(x + a/4)² + a²/8]
S = (a/2 + a - x)/2 × d = (3a/2 - x)/2 × √[(x + a/4)² + a²/8]
Giải S'(x) = 0 ⇒ x = 5a/8
Kết luận: x = 5a/8 thì diện tích HKMN nhỏ nhất
Cho mình xin 1 tick với ạ

Gọi số học sinh nam là x \(\Rightarrow\) nữ là \(30-x\) (\(2\le x< 30\))
Không gian mẫu: \(C_{30}^3\)
Số cách chọn ra 2 nam và 1 nữ: \(C_x^2.C_{30-x}^1\)
Xác suất: \(\frac{C_x^2C_{30-x}^1}{C_{30}^3}=\frac{12}{29}\)
\(\Rightarrow x=16\)
Vậy có 16 nam và 14 nữ

Số kết quả có thể là C520C205.
Số kết quả thuận lợi là số cách chọn 5 số trong tập [1,2,…,10][1,2,…,10]. Do đó, số kết quả thuận lợi là C510C105.
Vậy xác suất cần tìm là C510C520≈0,016
đúng ko