LC
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NK
8
5 tháng 11 2017
Ta có :
Bội của 4 là:
0, 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44,...
(thêm 4 để được bội số tiếp theo).
Bội của 6 là:
0, 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66,...
(thêm 6 để được bội số tiếp theo).
Bội chung của 4 và 6 là các số cùng xuất hiện trong hai dãy trên (không tính số 0):
12, 24, 36, 48,....
Vậy bội chung nhỏ nhất của 4 và 6 là 12
NH
2
22 tháng 11 2021
\(16=2^4;28=2^2\cdot7;40=2^3\cdot5\\ \RightarrowƯCLN\left(16,28,40\right)=2^2=4\\ BCNN\left(16,28,40\right)=2^4\cdot5\cdot7=560\)
22 tháng 11 2021
16=24 ; 28=22.7 ; 40=23.5
=> ước chung lớn nhất: 22
bội chung nhỏ nhất: 22.7.5=140
AH
Akai Haruma
Giáo viên
21 tháng 8 2023
Lời giải:
Ta có:
$4=2^2$
$6=2.3$
$\Rightarrow BCNN(4,6)=2^2.3=12$
$\Rightarrow BC(4,6)=\left\{0; 12; 24; 36; 48; 60; 72; 84; ...\right\}$
Suy ra BC nhỏ hơn 80 của $4,6$ là:
$\left\{0; 12; 24; 36; 48; 60; 72\right\}$
----------------------
$3=3$
$9=3^2$
$\Rightarrow BCNN(3,9)=9$
$\Rightarrow BC(3,9)=\left\{0; 9; 18; 27; 36; 45; 54; 63; 72; 81; 90; 99;...\right\}$
Vậy BC nhỏ hơn $90$ của $3,9$ là:
$\left\{0; 9; 18; 27; 36; 45; 54; 63; 72; 81\right\}$
24 tháng 10 2015
câu a; b cách làm tương tự nhau. Bạn xem câu ở câu hỏi tương tự: http://olm.vn/hoi-dap/question/89869.html
c) đề bài cho [a;b] + (a;b) = 15
gọi d = (a;b) => a = d.m; b = d.n ( coi m < n và m; n nguyên tố cùng nhau)
Ta có: [a;b] = \(\frac{a.b}{d}=\frac{dm.dn}{d}=d.m.n\)
khi đó, d.mn + d = 15 => d(m.n + 1) = 15 => m.n + 1 \(\in\) Ư(15) mà m.n + 1 > 2
=> m.n + 1 \(\in\) {3;5;15}
+) m.n + 1 = 3 => m.n = 2 = 1.2 => m = 1; n = 2 và d = 5 => a = 5.1 = 5; b = 5.2 = 10
+) m.n + 1 = 5 => m.n = 4 = 1.4 => m = 1; n = 4 và d = 3 => a = 3.1 = 3; b = 3.4 = 12
+) m.n + 1 = 15 => m.n = 14 =1 .14 = 2.7
m =1; n = 14 ; d = 1 => a= 1; b = 14
m = 2; n = 7 ;d = 1 => a = 2; b = 7
Vậy....
17 tháng 10 2021
a)45 = 32.5
204 = 22.3.17
126 = 2.32.7
=> UCLN(a;b;c) = 3
b)có BCNN(a;b;c) = 22.32.5.7.17 = 21420
=>BCNN:UCLN=21420:3=7140
=> BCNN chia hết cho UCLN
HT
CM
16 tháng 10 2018
a, BCNN(210;280) = 840 => BC(210;280) = 840k (k ∈ N)
b, BCNN(105;135) = 945 => BC(105;135) = 945k (k ∈ N)
c, BCNN(24;36) = 72 => BC(24;36) = 72k (k ∈ N)
d, BCNN(48;80;72) = 720 => BC(48;80;72) = 720k (k ∈ N)
e, BCNN(42;55;91) = 30030 => BC(42;55;91) = 30030k (k ∈ N)
f, BCNN(12;36;102) = 612 => BC(12;36;102) = 612k (k ∈ N)
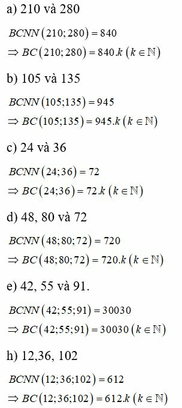
16={1;2;4;8;16}
80={1;2;4;5;8;10;16;20;40;80}
176={1;2;4;8;11;16;22;44;88;176}
ƯC(16;80;176)={1;2;4;8;16}
ƯCNN(16;80;176)=1
BCNN(16,80,176)=880