Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) <=>
Miền nghiệm của hệ bất phương trình là miền không bị gạch sọc ở hình bên (không kể các điểm).
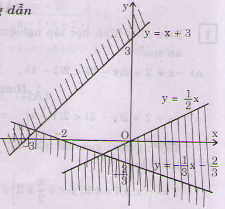
b) <=>
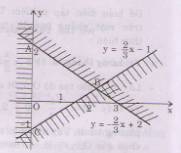
Miền nghiệm của hệ bất phương trình là miền tam giác ABC bao gồm cả các điểm trên cạnh AC và cạnh BC (không kể các điểm của cạnh AB).
a) \(\left\{{}\begin{matrix}2x-1\le0\\-3x+5< 0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\le\dfrac{1}{2}\\x>\dfrac{5}{3}\end{matrix}\right.\)\(\Leftrightarrow x\in\varnothing\).
b) Vẽ hai đường thẳng \(y=3;2x-3y+1=0\).
Vì điểm \(O\left(0;0\right)\) có tọa độ thỏa mãn bất phương trình \(2x-3y+1>0\) và không thỏa mãn bất phương trình \(3-y< 0\) nên phần không tô màu là miền nghiệm của hệ bất phương trình: \(\left\{{}\begin{matrix}3-y< 0\\2x-3y+1>0\end{matrix}\right.\).
TenAnh1
TenAnh1
A = (-4.34, -5.96)
A = (-4.34, -5.96)
A = (-4.34, -5.96)
B = (11.02, -5.96)
B = (11.02, -5.96)
B = (11.02, -5.96)
a) \(x^2\ge4x\)(1)
Nếu \(\left[{}\begin{matrix}x_1=0\\x_2=4\end{matrix}\right.\) \(\Rightarrow VT=VP\)
Nếu \(x< 0\Rightarrow VT>0;VP< 0\)=> \(VT>VP\)
Nếu 0<x<4 \(\Rightarrow VT< VP\)
nếu x> 4\(\Rightarrow VT>VP\)
Kết luận nghiệm BPT (1): \(\left[{}\begin{matrix}x\le0\\x\ge4\end{matrix}\right.\)
b)
(1) \(\Rightarrow\left[{}\begin{matrix}x< \dfrac{3-\sqrt{5}}{2}\\x>\dfrac{3+\sqrt{5}}{2}\end{matrix}\right.\)
(2) \(\Rightarrow-2\le x\le3\)
KL nghiệm
\(\left[{}\begin{matrix}-2\le x< \dfrac{3-\sqrt{5}}{2}\\\dfrac{3+\sqrt{5}}{2}< x\le3\end{matrix}\right.\)
a)\(Bpt\Leftrightarrow\) \(\left\{{}\begin{matrix}x^2-4x\ge0\left(1\right)\\\left(2x-1\right)^2-9>0\left(2\right)\end{matrix}\right.\)
Giải (1): \(x^2-4x\ge0\Leftrightarrow\left[{}\begin{matrix}x\ge4\\x\le0\end{matrix}\right.\)
Giải (2): \(\left(2x-1\right)^2-9=\left(2x-1\right)^2-3^2=\left(2x-4\right)\left(2x+2\right)\)
\(\left(2x-4\right)\left(2x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
Vì vậy: \(\left(2x-1\right)^2-9< 0\Leftrightarrow-1< x< 2\).
Kết hợp điều kiện \(\left(1\right)\) và \(\left(2\right)\) suy ra: \(-1< x\le0\) thỏa mãn hệ bất phương trình.
a)
\(\Leftrightarrow4m^2-4m+1-4\left(m^2-m-2\right)=9\ge0\Leftrightarrow\forall m\in R\)
b)
\(m^2-\left(2m^2+m-1\right)=-m^2-m+1< 0\)
\(\Leftrightarrow m^2+m-1>0\Rightarrow\left(m+\dfrac{1}{2}\right)^2-\dfrac{5}{4}\Rightarrow\left[{}\begin{matrix}m< \dfrac{-1-\sqrt{5}}{2}\\m>\dfrac{-1+\sqrt{5}}{2}\end{matrix}\right.\)
Thay \(x=-3\) vào bất phương trình (1) ta được:
\(3.\left(-3\right)+1< -3+3\)\(\Leftrightarrow-8< 0\) ( đúng)
Vậy \(x=-3\) là nghiệm của bất phương trình (1)
TThay \(x=-3\) vào bất phương trình (2) ta được:
\(\left(3.\left(-3\right)+1\right)^2< \left(-3+3\right)^2\)\(\Leftrightarrow64< 0\) (vô lý).
Vậy \(x=-3\) là nghiệm của bất phương trình (2).
Vậy hai bất phương trình (1) và (2) không tương đương và bình phương hai vế của bất phương trình không là phép biến đổi tương đương.
a, \(\left|5x-4\right|\ge6\)
\(\Leftrightarrow\left[{}\begin{matrix}5x-4\ge6\\5x-4\le-6\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x\ge2\\x\le-\dfrac{2}{5}\end{matrix}\right.\)
a) <=> (5x - 2)2 ≥ 62 <=> (5x – 4)2 – 62 ≥ 0
<=> (5x - 4 + 6)(5x - 4 - 6) ≥ 0 <=> (5x + 2)(5x - 10) ≥ 0
Bảng xét dấu:
Từ bảng xét dấu cho tập nghiệm của bất phương trình:
T = ∪ [2; +∞).
b) <=>
<=>
<=>
<=>
Tập nghiệm của bất phương trình T = (-∞; - 5) ∪ (- 1; 1) ∪ (1; +∞).
a)\(\left\{{}\begin{matrix}2m-1>0\Rightarrow m>\dfrac{1}{2}\left(1\right)\\m^2-\left(m-2\right)\left(2m-1\right)< 0\left(2\right)\end{matrix}\right.\)
\(\left(2\right)\Leftrightarrow m^2-\left(2m^2-m-4m+2\right)=-m^2+5m-2< 0\)
\(m^2-5m+2>0\Rightarrow\left[{}\begin{matrix}m< \dfrac{5-\sqrt{17}}{2}< \dfrac{1}{2}\\m>\dfrac{5+\sqrt{17}}{2}\end{matrix}\right.\)
Nghiệm hệ là
\(m>\dfrac{5+\sqrt{17}}{2}\)
b)\(\left\{{}\begin{matrix}m^2-m-2< 0\left(1\right)\\\left(2m-1\right)^2-4\left(m^2-m-2\right)\le0\left(2\right)\end{matrix}\right.\)
\(\left(2\right)\left(2m-1\right)^2-4\left(m^2-m-2\right)=9< 0,\forall m\).
Suy ra (2) vô nghiệm .
Kết luận hệ vô nghiệm.
a) - x + 2 + 2(y - 2) < 2(1 - x) <=> y <
Tập nghiệm của bất phương trình là:
T = {(x, y)|x ∈ R; y <
}.
Để biểu diễn tập nghiệm T trên mặt phẳng tọa độ, ta thực hiện:
+ Vẽ đường thẳng (d): y=
+ Lấy điểm gốc tọa độ O(0; 0)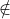
(d).
Ta thấy: 0 <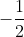
- 0 + 2. Chứng tỏ (0; 0) là một nghiệm của bất phương trình. Vậy nửa mặt phẳng bờ là đường thẳng (d) (không kể bờ) chứa gốc O(0; 0) là tập hợp các điểm biểu diễn tập nghiệm của bất phương trình đã cho (nửa mặt phẳng không bị gạch sọc)