Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta thấy đường thẳng \(y=ax+b\) đi qua hai điểm \(\left(0;3\right)\) và \(\left(1;0\right)\). Vậy ta có :
\(\left\{{}\begin{matrix}3=b\\0=a+b\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=3\end{matrix}\right.\)
Đường thẳng có phương trình là \(y=-3x+3\)
b) \(y=-4x\)
c) \(y=x-2\)

Gọi \(d=ƯCLN\left(8n+5;6n+4\right)\left(d\in Z\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}8n+5⋮d\\6n+4⋮d\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}24n+15⋮d\\24n+16⋮d\end{matrix}\right.\)
\(\Leftrightarrow1⋮d\)
Vì \(d\in Z;1⋮d\Leftrightarrow d=1\)
\(\LeftrightarrowƯCLN\left(8n+5;6n+4\right)=1\)
Vậy phân số \(\dfrac{8n+5}{6n+4}\) tối giản với mọi n
\(\rightarrowđpcm\)

a) ta có :
\(\Delta'=1^2-\left(-1-m\right)\left(m^2-1\right)=1-\left(-m^2+1-m^3+m\right)=1+m^2-1+m^3-m=m^3+m^2-m=m\left(m^2+m-1\right)\)để phương trình có nghiệm thì \(\Delta\ge0\)
hay \(m\left(m^2+m-1\right)\ge0\)
=> \(\left\{{}\begin{matrix}m\ge0\\m^2+m-1\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\ge0\\\left(m+\dfrac{1}{2}\right)^2-\dfrac{5}{4}\ge0\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}m\ge0\\\left(m+\dfrac{1}{2}\right)^2\ge\dfrac{5}{4}\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}m\ge0\\\left[{}\begin{matrix}m+\dfrac{1}{2}\ge\\m+\dfrac{1}{2}\le-\dfrac{\sqrt{5}}{2}\end{matrix}\right.\end{matrix}\right.\dfrac{\sqrt{5}}{2}}\)

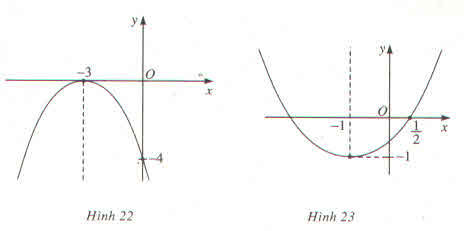
Hình 22
y=ax^2 +bx+c thỏa mãn hệ
\(\left\{{}\begin{matrix}y\left(0\right)=-4\Rightarrow c=-4\\y\left(-3\right)=9a-3b-4=0\\y\left(-6\right)=36a-6b-4=-4\end{matrix}\right.\)
(3) -(2) nhân 2
\(36a-18a-4+8=-4\Rightarrow18a=-8\Rightarrow a=\dfrac{-8}{18}=\dfrac{-4}{9}\)
Thế vào (2) -4-3b-4=0 => b=-8/3
Vậy pa ra bo; cho hình 22 là
\(y=-\dfrac{4}{9}x^2-\dfrac{8}{3}x-4\)

\(VT=\dfrac{1+cos2x}{cos2x}\times\dfrac{1+cos4x}{sin4x}\) (*)
Ta có: theo công thức hạ bậc có: \(cos^2x=\dfrac{1+cos2x}{2}\Leftrightarrow1+cos2x=2cos^2x\) (1)
Ta có: \(cos2x=1-sin^2x\Rightarrow cos4x=1-2sin^22x\) (2)
Tương Tự có \(sin2x=2sinx\times cosx\Rightarrow sin4x=2sin2x\times cos2x\) (3)
Thay (1),(2),(3) vào (*) ta được: \(VT=\dfrac{2cos^2x}{cos2x}\times\dfrac{1+\left(1-2sin^22x\right)}{2sin2x\times cos2x}\)
\(VT=\dfrac{2cos^2x\times2\left(1-sin^22x\right)}{cos^22x\times2sin2x}\) mà \(1-sin^22x=cos^22x\)
\(\Rightarrow VT=\dfrac{2cos^2x\times cos^22x}{cos^22x\times2sinx\times cosx}=\dfrac{cosx}{sinx}=tanx\left(đpcm\right)\)
đoạn cuối nhầm nha \(VT=\dfrac{cosx}{sinx}=cotx\left(đpcm\right)\)

C1:
\(A=\dfrac{10^{50}+2}{10^{50}-1}=\dfrac{10^{50}-1}{10^{50}-1}+\dfrac{3}{10^{50}-1}=1+\dfrac{3}{10^{50}-1}\\ B=\dfrac{10^{50}}{10^{50}-3}=\dfrac{10^{50}-3}{10^{50}-3}+\dfrac{3}{10^{50}-3}=1+\dfrac{3}{10^{50}-3}\\ \text{Vì }10^{50}-3< 10^{50}-1\Rightarrow\dfrac{3}{10^{50}-3}>\dfrac{3}{10^{50}-1}\Rightarrow1+\dfrac{3}{10^{50}-3}>1+\dfrac{3}{10^{50}-1}\Leftrightarrow B>A\)
Vậy \(B>A\)
C2: Áp dụng \(\dfrac{a}{b}>1\Rightarrow\dfrac{a}{b}>\dfrac{a+n}{b+n}\left(n>0\right)\)
Dễ thấy
\(B=\dfrac{10^{50}}{10^{50}-3}>1\\ \Rightarrow B=\dfrac{10^{50}}{10^{50}-3}>\dfrac{10^{50}+2}{10^{50}-3+2}=\dfrac{10^{50}+2}{10^{50}-1}=A\)
Vậy \(B>A\)

có cần phải tốn tiền v k pạn?quyền lợi của bn mà. trách nhiệm của quản lí và thầy cô là bảo vệ nk của bn


Đồ thị hàm số vuông góc với đường thẳng y = 4x + 1 nên 4.a = -1 hay
Đồ thị hàm số đi qua điểm N(4; -1) nên -1 = a.4 + b hay b = 0
Suy ra P = ab = 0
Chọn A.