Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a, \(\sqrt{13^2-12^2}=\sqrt{\left(13-12\right)\left(13+12\right)}\)
\(=\sqrt{1.25}=\sqrt{25}=5\)
b, \(\sqrt{17^2-8^2}=\sqrt{\left(17-8\right)\left(17+8\right)}\)
\(=\sqrt{9.25}=\sqrt{9}.\sqrt{25}=3.5=15\)
c, \(\sqrt{117^2-108^2}=\sqrt{\left(117-108\right)\left(117+108\right)}\)
\(=\sqrt{9.225}=\sqrt{9}.\sqrt{225}=3.15=45\)
d, \(\sqrt{313^2-312^2}=\sqrt{\left(313-312\right)\left(313+312\right)}\)
\(=\sqrt{1.625}=\sqrt{625}=25\)
Chúc bạn học tốt!!!
a, \(\sqrt{13^2-12^2}=\sqrt{\left(13-12\right)\left(13+12\right)}=\sqrt{25}=5\)
b, \(\sqrt{17^2-8^2}=\sqrt{\left(17-8\right)\left(17+8\right)}=\sqrt{9.25}=15\)
c, \(\sqrt{117^2-108^2}=\sqrt{\left(117-108\right)\left(117+108\right)}\)
\(=\sqrt{9.225}=45\)
d, \(\sqrt{313^2-312^2}=\sqrt{\left(313-312\right)\left(313+312\right)}=\sqrt{625}=25\)
a)\(\sqrt{\left(13+12\right)\left(13-12\right)}=\sqrt{25}+\sqrt{1}=5+1=6\)=6 ( hằng đẳng thức số 3) \(a^2-b^2=\left(a+b\right)\left(a-b\right)\)
b) tương tự
a) \(\sqrt{13^2-12^2}=\sqrt{\left(13-12\right)\left(13+12\right)}=\sqrt{25}=5\)
b) \(\sqrt{17^2-8^2}=\sqrt{\left(17-8\right)\left(17+8\right)}=\sqrt{25.9}=\sqrt{225}=15\)
c) \(\sqrt{117^2-108^2}=\sqrt{\left(117-108\right)\left(117+108\right)}=\sqrt{225.9}=\sqrt{2025}=45\)
d) \(\sqrt{313^2-312^2}=\sqrt{\left(313-312\right)\left(313+312\right)}=\sqrt{625}=25\)
mk nghi nhu vay ko biet co dung ko
dung thi bao mk nha
a) √54 = √9.6 = 3√6
b) √108 = √36.3 = 6√3
c) 0,1√20000 = 0,1√10000.2= 0,1.100√2 = 10√2
d) -0,05.√28800 = -0,05.√14400.2 = -0,05.120√2 = -6√2
e)√7.63.a2 = √7.7.9.a2 = 7.3|a| = 21|a|
a, \(\sqrt{3+2\sqrt{2}}=\sqrt{\sqrt{2}^2+2\sqrt{2}+1}=\sqrt{\left(\sqrt{2}+1\right)^2}=\left|\sqrt{2}+1\right|=\sqrt{2}+1\)
b, \(\sqrt{3-2\sqrt{2}}=\sqrt{\sqrt{2}^2-2\sqrt{2}+1}=\sqrt{\left(\sqrt{2}-1\right)^2}=\left|\sqrt{2}-1\right|=\sqrt{2}-1\)
c, \(\sqrt{8-2\sqrt{15}}=\sqrt{\sqrt{5}^2-2\sqrt{5.3}+\sqrt{3}^2}=\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}\)
\(=\left|\sqrt{5}-\sqrt{3}\right|=\sqrt{5}-\sqrt{3}\)
a: \(=\sqrt{9\cdot6}=3\sqrt{6}\)
b: \(=\sqrt{36\cdot3}=6\sqrt{3}\)
c: \(=\dfrac{1}{10}\cdot\sqrt{10000\cdot2}=\dfrac{1}{10}\cdot100\cdot\sqrt{2}=10\sqrt{2}\)
d: \(=-\dfrac{1}{20}\cdot\sqrt{14400\cdot2}=-\dfrac{1}{20}\cdot120\cdot\sqrt{2}=-6\sqrt{2}\)
e: \(=\sqrt{7\cdot7\cdot9\cdot a^2}=21\left|a\right|\)
a) Ta có:
5√15+12√20+√5515+1220+5
=√52.15+√(12)2.20+√5=√25.15+√14.20+√5=√255+√204+√5=√5+√5+√5=(1+1+1)√5=3√5=52.15+(12)2.20+5=25.15+14.20+5=255+204+5=5+5+5=(1+1+1)5=35
b) Ta có:
√12+√4,5+√12,512+4,5+12,5
=√12+√92+√252=√12+√9.12+√25.12=√12+√32.12+√52.12=√12+3√12+5√12=(1+3+5).√12=9√12=91√2=9.√22=9√22=12+92+252=12+9.12+25.12=12+32.12+52.12=12+312+512=(1+3+5).12=912=912=9.22=922
c) Ta có:
√20−√45+3√18+√72=√4.5−√9.5+3√9.2+√36.2=√22.5−√32.5+3√32.2+√62.2=2√5−3√5+3.3√2+6√2=2√5−3√5+9√2+6√2=(2√5−3√5)+(9√2+6√2)=(2−3)√5+(9+6)√2=−√5+15√2=15√2−√520−45+318+72=4.5−9.5+39.2+36.2=22.5−32.5+332.2+62.2=25−35+3.32+62=25−35+92+62=(25−35)+(92+62)=(2−3)5+(9+6)2=−5+152=152−5
d) Ta có:
0,1√200+2√0,08+0,4.√50=0,1√100.2+2√0,04.2+0,4√25.2=0,1√102.2+2√0,22.2+0,4√52.2=0,1.10√2+2.0,2√2+0,4.5√2=1√2+0,4√2+2√2=(1+0,4+2)√2=3,4√2
a) \(21-8\sqrt{5}=16-2\times4\times\sqrt{5}+5=\left(4-\sqrt{5}\right)^2\)
b) \(47-12\sqrt{11}=36-2\times6\times\sqrt{11}+11=\left(6-\sqrt{11}\right)^2\)
c) \(13-4\sqrt{3}=12-2\times1\times\sqrt{3}+1=\left(2\sqrt{3}-1\right)^2\)
d) \(43+30\sqrt{2}=25+2\times5\times3\sqrt{2}+18=\left(5+3\sqrt{2}\right)^2\)
e) \(41+24\sqrt{2}=9+2\times3\times4\sqrt{2}+32=\left(3+4\sqrt{2}\right)^2\)
g) \(29-12\sqrt{5}=9+2\times3\times2\sqrt{5}+20=\left(3+2\sqrt{5}\right)^2\)
h) \(49-8\sqrt{3}=48-2\times4\sqrt{3}\times1+1=\left(4\sqrt{3}-1\right)^2\)
i) \(37-12\sqrt{7}=28-2\times3\times2\sqrt{7}+9=\left(2\sqrt{7}-3\right)^2\)
a) ĐS: 5.
b)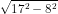
= 
= 
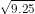= √9.√25 = 3.5 = 15.
c) ĐS: 45
d) ĐS: 25
a. \(\sqrt{13^2-12^2}\)
=\(\sqrt{\left(13+12\right).\left(13-12\right)}\)
=\(\sqrt{25.1}\)
=\(\sqrt{25}.\sqrt{1}\)
=5.1
=5
b. \(\sqrt{17^2-8^2}\)
=\(\sqrt{\left(17+8\right).\left(17-8\right)}\)
=\(\sqrt{25.9}\)
=\(\sqrt{25}.\sqrt{9}\)
=5.3
=15
c. \(\sqrt{117^2-108^2}\)
=\(\sqrt{\left(117+108\right).\left(117-108\right)}\)
=\(\sqrt{225.9}\)
=\(\sqrt{225}.\sqrt{9}\)
=15.3
=45
d. \(\sqrt{313^2-312^2}\)
=\(\sqrt{\left(313+312\right).\left(313-312\right)}\)
=\(\sqrt{625.1}\)
=\(\sqrt{625}.\sqrt{1}\)
=25.1
=25
c.\(\sqrt{117^2-108^2}\)