K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
1 tháng 5 2020
a) dấu hiệu điều tra là vấn đề hay hiện tượng mà người điều tra quan tâm tìm hiểu
b)tần số của 1 giá trị là số lần xuất hiện của giá trị trong dãy giá trị của dấu hiệu được gọi là tần số của giá trị đó
c)tổng các tần số là tổng số lần xuất hiện của các giá trị
chúc bạn học tốt !!!
26 tháng 8 2017
\(\frac{x}{3}\)= \(\frac{y}{5}\) và x + y = 16
Áp dụng tính chất dãy tỉ bằng nhau ta có:
\(\frac{x}{3}\)= \(\frac{y}{5}\)=\(\frac{x+y}{3+5}\)= \(\frac{16}{8}\)=2
Suy ra : \(\frac{x}{3}\)= 2\(\Rightarrow\)x=6
\(\frac{y}{5}\)= 2\(\Rightarrow\)y=10
Vậy...
HT
0
28 tháng 6 2019
Đề là \(\Delta ABD,\Delta ACE\) vuông cân tại B và C hả?Nếu ko thì sai đề nhé.vẽ hình ra là bt ngay.Nếu đúng như t nói thì chờ tí khoảng chiều nay t ans cho
28 tháng 6 2019
a.
Theo tính chất góc ngoài của tam giác,ta có:
\(\widehat{KAB}=\widehat{ABH}+\widehat{BHA}=\widehat{ABH}+90^0\)
Mà \(\widehat{DBC}=\widehat{DBK}+\widehat{KBC}=90^0+\widehat{KBC}\)
\(\Rightarrow\widehat{KAB}=\widehat{DBC}\)
Xét \(\Delta ABK\) và \(\Delta BCD\) có:
\(AB=BD\)
\(\widehat{KAB}=\widehat{DBC}\left(cmt\right)\)
\(BC=AK\)
Khi đó \(\Delta ABK=\Delta BCD\left(c.g.c\right)\)
b.
Do \(\Delta ABK=\Delta BCD\left(c.g.c\right)\) nên \(\widehat{BKA}=\widehat{DCB}\left(2\right)\)
Mặt khác \(\widehat{HBK}+\widehat{KBH}=90^0\left(1\right)\)
Gọi giao điểm của KB và DC là F.
Từ (1);(2) suy ra \(\widehat{FBC}+\widehat{BCF}=90^0\Rightarrow\widehat{F}=90^0\)
\(\Rightarrow CD\perp BK\)
Chứng minh tương tự ta cũng có được \(BE\perp CK\)
Nếu bạn ko muốn dùng phép tương tự thì bạn chứng minh \(\Delta KAC=\Delta BCE\left(c.g.c\right)\)
\(\Rightarrow\widehat{ACK}=\widehat{CEB}\)
Gọi giao điểm của BE và CK là N.
Mà \(\widehat{ACK}+\widehat{NCE}=90^0\Rightarrow\widehat{NCE}+\widehat{NEC}=90^0\Rightarrow\widehat{N}=90^0\)
\(\Rightarrow BE\perp CK\)
c.
Xét \(\Delta KBC\) có 3 đường cao \(AH,BE,CD\) nên chúng đồng quy.
??
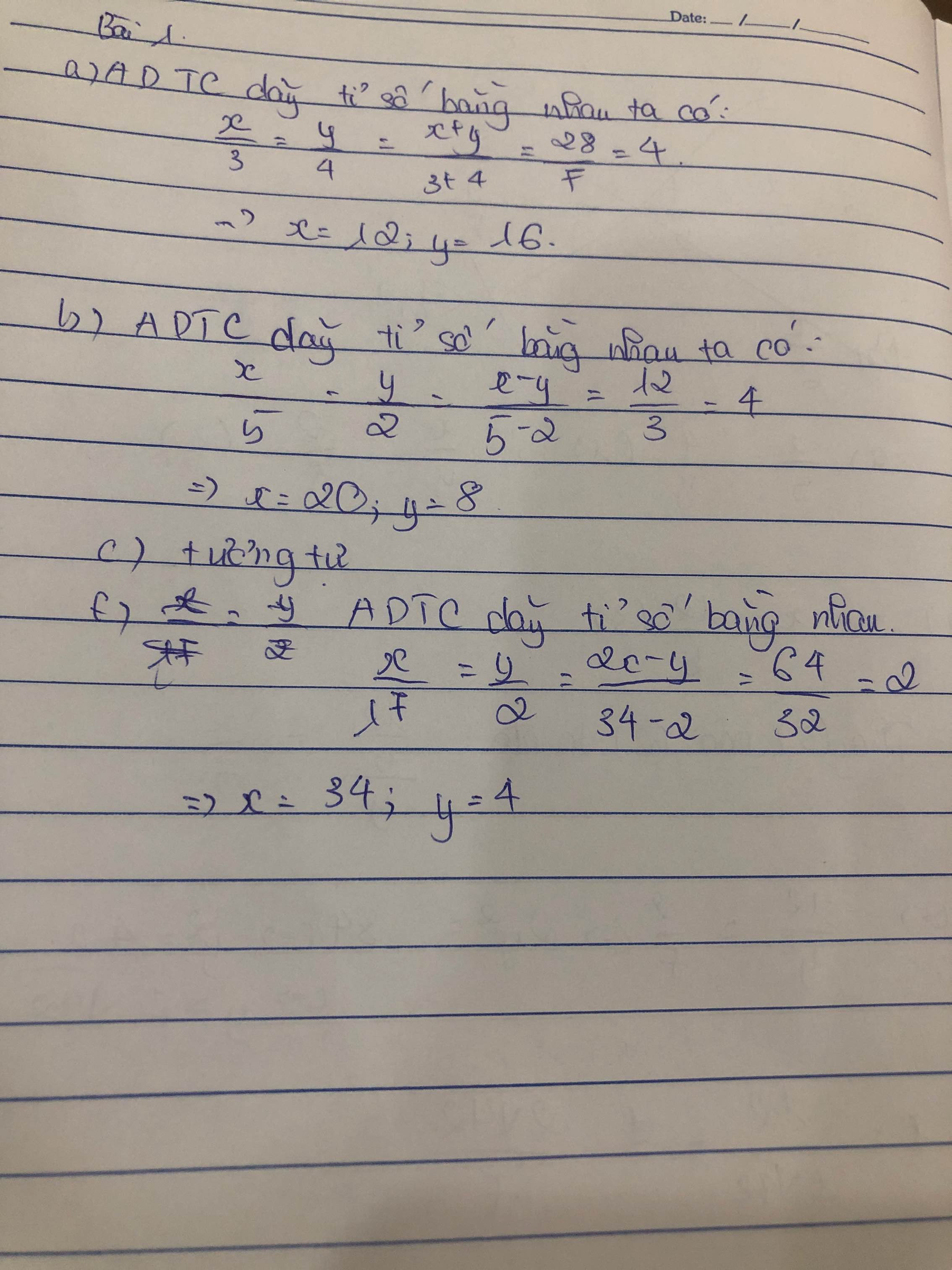
bày?