Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

3. Xét tam giác ADM và tam giác AEM có :
góc ADM = góc AEM = 90 độ
Góc BAM = góc CAM (gt)
AM chung
=>Tam giác ADM = tam giác AEm (c.huyền - g.nhọn)
=>MD = ME (cặp cạnh t/ứng )
AD = AE (cặp cạnh t/ứng )
Xét tam giác MDB và tam giác MEC có :
MB = MC (gt)
góc MDB = góc MEC = 90 độ
MD = ME ( câu a)
=>Tam giác MDB = Tam giác MEC (c.huyền-c.g.vuông)
Vì AD + DB = AB
AE + EC = AC
Mà AD = AE
DB = EC
=>AB = AC
Xét tam giác ABM và tam giác ACM có
AM chung
góc BAM = góc CAM (gt)
AB = AC (CMT)
=>Tam giác ABM = Tam giác ACM (c.huyền-g.nhon)
Vậy có 3 cặp tam giác bằng nhau



Cách giải chung. Đặt \(\frac{a}{b}=\frac{c}{d}=k\Rightarrow a=bk,c=dk\).
5. \(\frac{5a}{a+b}=\frac{5bk}{bk+b}=\frac{5k}{k+1}\)
\(\frac{5c}{c+d}=\frac{5dk}{dk+d}=\frac{5k}{k+1}\)
Suy ra đpcm.
6. \(\frac{a^2+3ab}{a^2-3b^2}=\frac{\left(bk\right)^2+3bk.b}{\left(bk\right)^2-3b^2}=\frac{k^2+3k}{k^2-3}\)
\(\frac{c^2+3cd}{c^2-3d^2}=\frac{\left(dk\right)^2+3dk.d}{\left(dk\right)^2-3d^2}=\frac{k^2+3k}{k^2-3}\)
Suy ra đpcm.
7, 8. Bạn làm tương tự.

ta có : Do NB song song với MA nên
\(\hept{\begin{cases}\widehat{ABN}+\widehat{MAB}=180^0\\\widehat{ABN}-\widehat{MAB}=40^0\end{cases}}\Rightarrow2\widehat{MAB}=180^0-40^0=140^0\)
Nên \(\widehat{MAB}=70^0\)

a) Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{2}=\frac{y}{3}=\frac{z}{5}=\frac{x+y+z}{2+3+5}=\frac{90}{10}=9\)
\(\Leftrightarrow\hept{\begin{cases}x=9.2=18\\y=9.3=27\\z=9.5=45\end{cases}}\)
b) \(2x=3y\Leftrightarrow\frac{x}{15}=\frac{y}{10},2y=5z\Leftrightarrow\frac{y}{10}=\frac{z}{4}\)
suy ra \(\frac{x}{15}=\frac{y}{10}=\frac{z}{4}\).
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{15}=\frac{y}{10}=\frac{z}{4}=\frac{x-z}{15-4}=\frac{11}{11}=1\)
\(\Leftrightarrow\hept{\begin{cases}x=15.1=15\\y=10.1=10\\z=4.1=4\end{cases}}\)
c) \(\frac{x}{y}=\frac{3}{4}\Leftrightarrow\frac{x}{9}=\frac{y}{12},\frac{y}{z}=\frac{3}{5}\Leftrightarrow\frac{y}{12}=\frac{z}{20}\)
suy ra \(\frac{x}{9}=\frac{y}{12}=\frac{z}{20}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{9}=\frac{y}{12}=\frac{z}{20}=\frac{2x-3y+z}{2.9-3.12+20}=\frac{6}{2}=3\)
\(\Leftrightarrow\hept{\begin{cases}x=3.9=27\\y=3.12=36\\z=3.20=60\end{cases}}\)
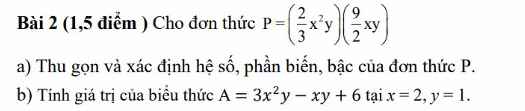

 M.n giải hộ em vs đg cần gấp ạ
M.n giải hộ em vs đg cần gấp ạ



 Giúp mình làm mấy câu tô màu vàng được ko ạ?Mình cảm ơn ạ!
Giúp mình làm mấy câu tô màu vàng được ko ạ?Mình cảm ơn ạ!




\(a,P=\left(\dfrac{2}{3}x^2y\right)\left(\dfrac{9}{2}xy\right)=3x^3y^2\)
Hệ số:3
Biến:x3y2
Bậc: 5
b, Thay x=2,y=1 vào A ta có:
\(A=3x^2y-xy+6=3.2^2.1-2.1+6=12-2+6=16\)
mình cảm ơn