K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MK
4
MN
29 tháng 7 2021
Chuyển cho tổng các miếng bìa trong hộp bằng 4.
=> Chỉ cần chuyển miếng bìa có chữ số 2 từ hộp thứ ba sang hộp thứ nhất
MN
16 tháng 5 2021
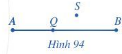
a) Hình 94:
Điểm A, Q, B thẳng hàng, điểm Q nằm giữa A và B
b) Hình 94:
Ba điểm không thẳng hàng A, Q, S hoặc A, B, S hoặc Q, B, S
c)
giải giùm tớ nha
DH
14 tháng 5 2017
Từ đề bài ta có:
\(T=\dfrac{1+2}{2}.\dfrac{1+3}{3}.\dfrac{1+4}{4}...\dfrac{1+98}{98}.\dfrac{1+99}{99}\)
\(=\dfrac{3}{2}.\dfrac{4}{3}.\dfrac{5}{4}...\dfrac{99}{98}.\dfrac{100}{99}\)
\(=\dfrac{100}{2}\)
\(=50\).
JH
15 tháng 5 2017
\(T=\left(\dfrac{1}{2}+1\right)\left(\dfrac{1}{3}+1\right)\left(\dfrac{1}{4}+1\right)...\left(\dfrac{1}{98}+1\right)\left(\dfrac{1}{99}+1\right)\)
\(T=\dfrac{3}{2}.\dfrac{4}{3}.\dfrac{5}{4}....\dfrac{99}{98}.\dfrac{100}{99}\)
\(T=\dfrac{3.4.5......99}{3.4.5......99}.\dfrac{100}{2}\)
\(T=50\)
TM
0
Bạn hãy trả lời đầy đủ?
Gọi số vịt là x (\(x \in {\mathbb{N}^*},\,\,x < 200\)).
Vì hàng 5 xếp thiếu 1 con nên x chia 5 dư 4=> x có chữ số tận cùng là 4 hoặc 9.
Vì hàng 2, hàng 4 không xếp được, do đó x không chia hết được cho 2 và cho 4 .
=> x có chữ số tận cùng là 9.
Vì số vịt xếp được thành 7 hàng nên x\( \vdots \)7.
Do đó x ∈ B(7), x có chữ số tận cùng là 9 và x < 200, nên x ∈ {49; 119; 189}.
Mà x chia cho 3 dư 1 nên x = 49.
Vậy có 49 con vịt.